Bayesova analýza
Bayesova analýza je metoda stanovení relativní pravděpodobnosti dvou nebo více alternativních možností, založená na Bayesově teorému pravděpodobnosti. V genetickém poradenství ji lze uplatnit při stanovování rizika v rodině, kde je genotyp některých relevantních příbuzných probanda neznámý (nelze ho jednoduše diagnostikovat), a nemůžeme u nich proto jasně stanovit přenašečství.
Využití[upravit | editovat zdroj]
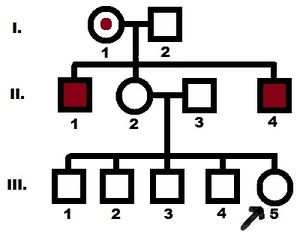
Využití Bayesovy analýzy v genetickém poradenství lze ilustrovat na příkladu rodiny s výskytem hemofilie A, jejíž rodokmen je zobrazen. Pro stanovení pravděpodobnosti přenašečství u III-5 je relevantní informací, zda II-2 je nebo není přenašečkou. Tento údaj ze zjištěných informací nelze stanovit, ale intuice napovídá, že pokud má III-5 čtyři zdravé bratry, pravděpodobnost, že jejich matka je přenašečkou, to patrně snižuje. Údaje podobného charakteru nám pomáhá zohlednit právě Bayesova analýza, bere totiž v úvahu určité důležité fenotypové informace.
Postup výpočtu[upravit | editovat zdroj]
Vypočítáme zvlášť pravděpodobnost II-2 pro obě hypotézy (varianty), tedy "II-2 je přenašečka" a "II-2 není přenašečka", v přehledné tabulce o dvou sloupcích. U obou hypotéz dále stanovíme postupně hodnoty následujících pravděpodobností: Apriorní pravděpodobnost je výchozí pravděpodobnost každé hypotézy, že je správná, aniž bychom věděli cokoliv dalšího o rodokmenu dané rodiny, než, co z něj zřejmě vyplývá.
- Jaká je pravděpodobnost, že II-2 je/není přenašečkou? II-2 je dcerou přenašečky, proto P(nepřenašečka) = ½, P(přenašečka) = ½.
Podmíněná pravděpodobnost je v každém sloupci, pod hypotézou pro tento sloupec, že události, o nichž víte, že se už staly (tj. skutečnosti, které jste o rodokmenu zjistili), se mohly odehrát za předpokladu, že hypotéza na začátku sloupce je správná.
- Jaká je pravděpodobnost, že II-2 má čtyři zdravé syny pro obě hypotézy? Pravděpodobnost, že se přenašečce narodí zdravý syn je ½, čtyři zdraví synové (½)4. Pravděpodobnost, že se „nepřenašečce“ narodí zdravý syn je 1, čtyři zdraví synové 4 × 1.
Celková pravděpodobnost je produktem apriorní a podmíněné pravděpodobnosti.
- Vypočítáme ji vynásobením apriorní a podmíněné pravděpodobnosti, viz příslušnou buňku v tabulce.
Aposteriorní pravděpodobnost staví obě celkové pravděpodobnosti proti sobě.
- Je poměrem celkové pravděpodobnosti hypotézy k součtu obou celkových pravděpodobností našich hypotéz. Z toho také vyplývá, že teprve hodnoty aposteriorní pravděpodobnosti dávají dohromady 1.
Nyní již dokážeme jednoduše vypočítat riziko pro probandku:
| hypotéza 1 | hypotéza 2 | |
|---|---|---|
| II/2 JE přenašečka | II/2 NENÍ přenašečka | |
| apriorní pravděpodobnost | 1/2 | 1/2 |
| podmíněná pravděpodobnost | 1 | |
| celková pravděpodobnost | ||
| aposteriorní pravděpodobnost |
- riziko přenašečství u II-2: 1/17
- riziko přenašečství u probandky (III-5): ½ × 1/17 = 1/34
Shrnutí[upravit | editovat zdroj]
Za využití fenotypových informací z rodokmenu jsme dokázali stanovit konkrétní hodnotu pravděpodobnosti, že matka probandky je přenašečkou hemofilie A, a tak kvantifikovat, co se zdálo být intuitivně pravděpodobné z pohledu na rodokmen. Uvedený příklad slouží pro ilustraci, podrobnější a složitější případy řeší například zdrojová literatura.
Odkazy[upravit | editovat zdroj]
Související články[upravit | editovat zdroj]
Použitá literatura[upravit | editovat zdroj]
- NUSSBAUM, Robert, Roderick MCINNES a Huntington WILLARD, et al. Klinická genetika : Thompson & Thompson. 1. vydání. Praha : Triton, 2004. 492 s. ISBN 978-80-7254-475-2.