Fórum:Testy/Položková analýza
Jak poznám špatnou otázku? Špatnou otázku může zkušený pedagog odhalit už v rámci oponentury testu. Nejlépe ji ale identifikují sami studenti – tím, jak na ni odpovídají. Vyplatí se proto odpovědi studentů analyzovat a hodnotit z nich vlastnosti položek. Výhoda je, že takovou položkovou analýzu můžeme (obzvlášť v rámci elektronického testování) snadno automatizovat, nemusí ji tedy provádět sám pedagog. Postačí, pokud výsledkům položkové analýzy rozumí a umí z nich vyvodit správné závěry.
Položkovou analýzu je vhodné provést už před ostrým nasazením testu, zadáme-li položky vybranému vzorku studentů v rámci pilotního testování. Při pilotním testování je potřeba zajistit, aby testovaný vzorek studentů co nejlépe odpovídal populaci studentů, pro které je test určen. Položková analýza by měla být prováděna také po ostrém testování na cílové skupině studentů.
U testových úloh sledujeme především jejich obtížnost a jejich citlivost neboli rozlišovací schopnost. Obtížnost popisuje, jaké procento testované skupiny odpoví správně. Citlivost říká, nakolik je položka schopná rozlišit mezi lepšími a horšími studenty. Studenty přitom na lepší a horší dělíme většinou podle celkového výsledku v testu, lze ale usuzovat také na základě jiného kritéria, např. na základě úspěšnosti v následném studiu apod. Na správně formulovanou položku by lepší studenti měli odpovídat správně častěji než studenti slabší.
Obtížnost a citlivost jdou ruku v ruce. Velmi obtížné a velmi snadné úlohy mívají malou rozlišovací schopnost, proto by jich obzvláště v testu, který má za cíl rozlišit testované studenty (např. přijímací testy), nemělo být příliš mnoho. Jednu nebo dvě velmi snadné úlohy lze použít v úvodu testu za účelem uklidnění žáků a zvýšení jejich motivace. Obtížnost dalších položek by v optimálním případě měla mít vzrůstající tendenci.
Další důležitou vlastností položky je její férovost. Položka by neměla zvýhodňovat některé skupiny studentů. Stejně chytří a stejně dobře připravení studenti různých skupin (děleno dle pohlaví, etnika apod.) by měli správnou odpověď na položku volit zhruba stejně často.
Položka je také podezřelá, pokud ji vynechalo větší množství studentů. Pokud se takové položky vyskytují na konci testu, může být kromě obtížnosti položek důvodem také příliš krátká doba stanovená k řešení testu (blíže viz kapitola 8.3.4 Analýza vynechaných odpovědí).
U výběrových úloh s distraktory (tj. „nesprávnými odpověďmi“) je potřeba zkontrolovat také vlastnosti jednotlivých nabízených odpovědí. Distraktory, které nejsou dostatečně atraktivní (volilo je příliš malé procento studentů), nebo které dostatečně nerozlišují mezi horšími a lepšími studenty, je potřeba nahradit jinými.
Podívejme se nyní blíže na jednotlivé nástroje položkové analýzy.
Obtížnost položky[upravit | editovat zdroj]
Není položka příliš snadná nebo příliš těžká?
Obtížnost testových úloh typu ano/ne se obvykle odhaduje jako podíl respondentů, kteří na danou úlohu odpověděli správně. Odhadu se říká index obtížnosti a značí se :
- .
Index obtížnosti nabývá hodnot mezi 0 a 1. Je tím blíže 1, čím víc studentů na položku zodpovědělo správně. Spíš bychom tedy měli mluvit o „snadnosti položky“. Někteří autoři proto zavádějí ještě hodnotu obtížnosti. Hodnota obtížnosti je daná procentuálním zastoupením žáků, kteří na položku odpověděli nesprávně, jde tedy o doplněk indexu obtížnosti:
- .
V případě bodované položky, za kterou lze dosáhnout 0 až bodů, se index obtížnosti obecněji definuje pomocí aritmetického průměru bodových hodnocení všech žáků v dané úloze:
- .
Velmi obtížné ( < 0,2) a velmi snadné ( > 0,8) úlohy mívají malou rozlišovací schopnost, proto by jich v testu nemělo být příliš mnoho. Malé množství velmi snadných úloh lze použít v úvodu testu za účelem uklidnění žáků a zvýšení jejich motivace. Obzvláště pro testy, jejichž cílem je rozlišit testované studenty (např. přijímací testy), jsou optimální položky s obtížností okolo 0,5.
Je potřeba zdůraznit, že zde zavedený odhad obtížnosti je závislý na testované populaci. Budeme-li obtížnost odhadovat na základě odpovědí skupiny chytřejších studentů, bude se položka jevit jako snazší. Výše uvedený klasický odhad je proto platný vždy jen pro vzájemně podobné skupiny studentů. Hodí se např., pokud test každoročně dáváme srovnatelným skupinám studentů. Problém nastává, pokud položky využíváme např. pro různé studijní obory, na více školách apod. Obecnější přístup, kdy se obtížnost položky definuje v závislosti na schopnostech testovaných studentů, používá tzv. teorie odpovědi na položku.
Citlivost položky[upravit | editovat zdroj]
Rozlišuje položka dobře mezi lepšími a horšími studenty?
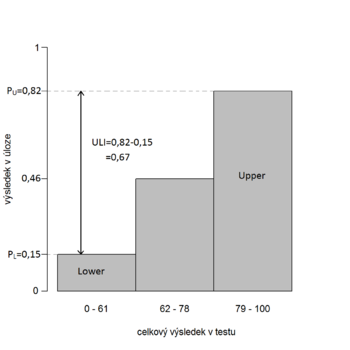
Citlivost neboli diskriminační schopnost vypovídá o schopnosti položky rozlišovat mezi lepšími a horšími studenty. Jedním ze způsobů odhadu citlivosti je tzv. upper-lower index (ULI). Počítá se jako rozdíl úspěšnosti v položce mezi skupinou lepších (U – upper) a horších (L – lower) studentů:
- ,
viz také obr. 8.4. Studenti jsou zpravidla děleni do dvou podobně velkých skupin (optimálně na polovinu) na základě celkového počtu bodů v testu.
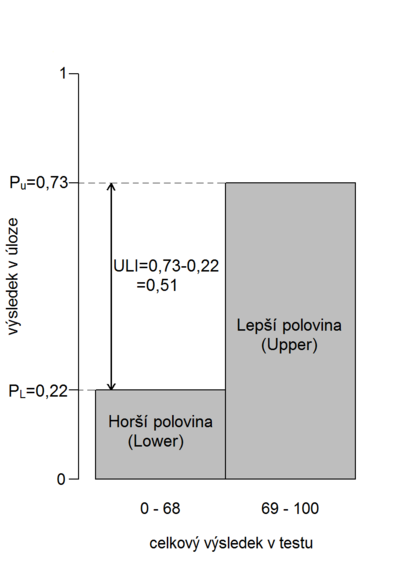
ULI nabývá hodnot mezi −1 a 1. Hodnoty ULI blízké 1 mají úlohy, které dobří žáci řeší správně a slabší žáci řeší nesprávně. Nulovou hodnotu mají úlohy, které obě skupiny žáků řeší stejně dobře. Úlohy se záporným indexem ULI zvýhodňují slabší studenty. Mohou to být úlohy s komplikovaným zadáním, které se lepší žáci neúspěšně pokoušejí řešit, zatímco horší je s větším štěstím správně uhodnou. Úlohy se zápornou citlivostí by se v testu neměly objevovat. U položek příliš snadných nebo příliš obtížných (kterých by obzvláště v rozlišovacím testu nemělo být mnoho) lze očekávat nízkou rozlišovací schopnost. Byčkovský v [1] dále uvádí, že
- pro položky s obtížností mezi 0,2 a 0,3 a obtížností mezi 0,7 a 0,8 je za podezřelé potřeba považovat úlohy s citlivostí ULI < 0,15,
- pro úlohy s obtížností mezi 0,3 a 0,7 se za podezřelé považují již položky s rozlišovací schopností ULI < 0,25.
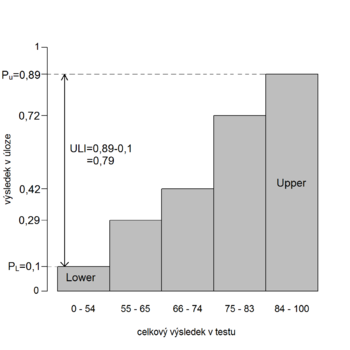
Jelikož prostřední hodnoty celkového skóre v testu může dosáhnout současně více studentů, vyvstává otázka, jak s těmito studenty při dělení na polovinu naložit. Je možné zařadit je do jedné ze skupin (ale do které?), nebo rozdělit (ale jak?) a část zařadit mezi lepší a část mezi horší, nebo jednoduše vynechat. V některých zdrojích se ULI také definuje jako rozdíl mezi nejlepší a nejhorší třetinou studentů (viz obr. 8.5a), čímž se prostředním hodnotám často zcela vyhneme. Lze obecně uvažovat i jiné podíly, např. krajní pětiny studentů (viz obr. 8.5b). Systém Rogo počítá ULI na základě dolních a horních 27,5 % studentů. Indexy ULI vycházejí v případě menších porovnávaných skupin zpravidla větší (jedná se pak o rozdíl v úspěšnosti ve dvou více rozdílných skupinách), a proto by pro ně měla být požadována o něco větší hodnota než při klasickém rozdělení na dvě části. I pro tyto definice však platí, že podezřelé jsou hodnoty záporné a hodnoty blízké 0.
Grafy: Další možná pojetí ULI
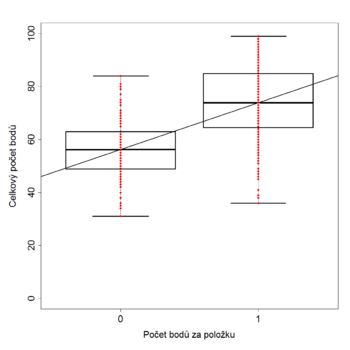
Jiným přístupem pro hodnocení citlivosti binární položky (tj. položky typu ano/ne) je porovnat průměrný bodový výsledek u skupiny, která položku zodpověděla správně (), s bodovým výsledkem u skupiny, která položku zodpověděla nesprávně (). Na dobře fungující položku by měli správně odpovídat vesměs dobří studenti, průměrný výsledek u studentů ze skupiny by proto měl být vyšší než u studentů ze skupiny . Významnost rozdílů průměrných bodových výsledků lze testovat dvouvýběrovým t testem [2], ekvivalentně také testem nenulovosti korelačního koeficientu mezi počtem bodů za položku (zde 0 nebo 1) a celkovým počtem bodů.
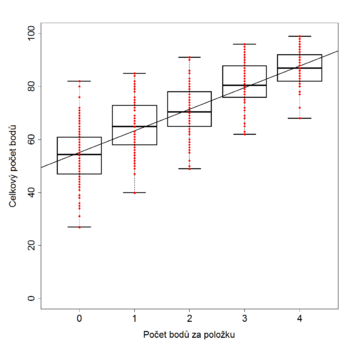
Zobecněním na bodované položky je tzv. index RIT. Jde o Pearsonův korelační koeficient (značený často ) mezi položkou (item, I) a počtem bodů v celém testu (T). Pro položku, která dobře rozlišuje mezi horšími a lepšími studenty (měřeno počtem bodů v testu) je koeficient RIT blízký jedné. Pro položky, které mezi lepšími a horšími studenty nerozlišují, je tento koeficient blízký nule. Záporné koeficienty pak upozorňují na položky, které zvýhodňují slabší studenty.
Jelikož počet bodů za položku ovlivní celkový počet bodů, hodnoty nejsou nezávislé. Formálně správnější je proto hodnotit korelaci mezi položkou a součtem bodů za zbylé položky (angl. rest). Tento Pearsonův korelační koeficient je číselně blízký předchozímu a nazývá se index RIR.
Graf: Diskriminační index RIT
Používanou charakteristikou konzistence položek je také Cronbachovo alfa testu po vynechání položky: nekonzistentní položky poznáme tak, že po jejich vynechání reliabilita testu měřená Cronbachovým alfa stoupne.
I zde je na místě připomenout, že zavedené indexy citlivosti jsou závislé na testované skupině studentů. Vztaženo k již zmiňovanému příkladu z přijímacích zkoušek, budeme-li analyzovat data všech studentů, kteří se zkoušky zúčastnili, díky menší homogenitě testovaných lze předpokládat, že položky budou studenty rozlišovat lépe. Budeme-li analyzovat pouze data skupiny studentů, kteří byli přijati ke studiu, rozlišovací schopnost bude u této homogennější skupiny patrně nižší. Pro obecnější pojetí opět odkazujeme na kapitolu věnovanou teorii odpovědi na položku, kde je diskriminační schopnost zavedena ve vztahu k celkové schopnosti studenta.
Citlivost jako validita položky[upravit | editovat zdroj]
Dosud jsme zkoumali vztah úspěšnosti v položce k celkovému výsledku. Uvědomme si, že tato citlivost odráží, do jaké míry jsou položky vnitřně konzistentní – má tedy co do činění s reliabilitou testu.
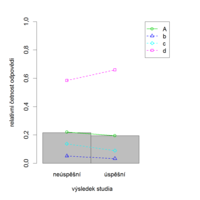
Pokud by nás zajímala citlivost položky vzhledem k nějakému jinému kritériu, např. závěrečné známce z předmětu, celkové úspěšnosti ve studiu nebo úspěšnosti v zaměstnání, zajímáme se tak potažmo o validitu dané položky. Položka přitom, stejně jako celý test, může dobře rozlišovat mezi studenty co do celkového počtu bodů v testu, ale nemít žádný vztah ke zkoumanému kritériu (např. budoucí úspěšnosti ve studiu).
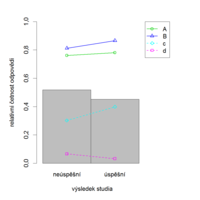
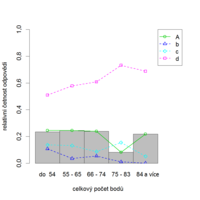
Citlivost ve smyslu validity položky můžeme reprezentovat také pomocí indexu ULI, studenty však na horší a lepší dělíme podle zkoumaného kritéria (tedy např. dle průměrné známky v následujícím studiu, úspěšnosti apod.) Lze také použít korelačních koeficientů mezi položkovým skóre a zkoumaným kritériem. Obecněji lze závislost uchopit pomocí regresních modelů, jak bylo zmíněno v části věnované validitě testu.
Validita jednotlivých položek nám pak může pomoci vypátrat, které typy položek způsobují nízkou validitu celého testu.
Analýza vynechaných odpovědí[upravit | editovat zdroj]
Pokud vysoké procento studentů na určitou položku neodpoví, může to ukazovat na její obtížnost, ale také nesrozumitelnost. Za podezřelé je nutné považovat všechny položky, které vynechalo více než 20 % respondentů. Pokud se na konci testu objevuje souvislá řada nezodpovězených položek, lze předpokládat, že je studenti nestihli vyřešit z časových důvodů. V takovém případě je potřeba zvážit zkrácení testu nebo prodloužení doby na řešení.
Počet vynechaných odpovědí souvisí také s hodnocením testu. Vyšší procento vynechaných odpovědí lze předpokládat u testů, které penalizují nesprávnou odpověď (nepenalizují-li vynechání odpovědi ještě více).
Grafická interpretace vlastností položky[upravit | editovat zdroj]
Na vlastnosti položky se můžeme podívat detailněji, rozdělíme-li studenty podle úspěšnosti na několik skupin a úspěšnost v dané položce zobrazíme pro každou skupinu zvlášť. Tato metoda je jakýmsi úvodem k přístupu tzv. teorie odpovědi na položku (item response theory, IRT), který bude prezentován v následující části.
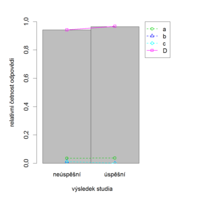
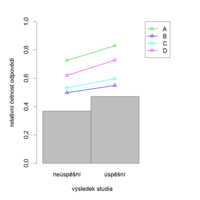
Někdy se stává, že kritérium, podle kterého dělíme studenty na lepší a horší, je jen dvouhodnotové. Stává se to například, když hodnotíme citlivost položky vzhledem k celkové úspěšnosti následného studia (tj. „dokončil studium / nedokončil studium“). Menší počet skupin použijeme také, máme-li malý počet respondentů. V tom případě bývá lépe studenty rozdělit jen na dvě nebo tři skupiny.
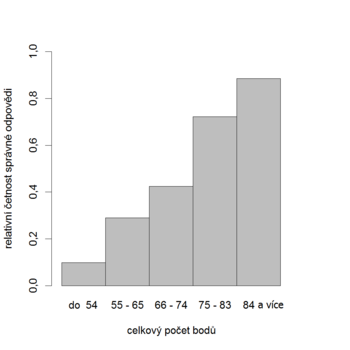
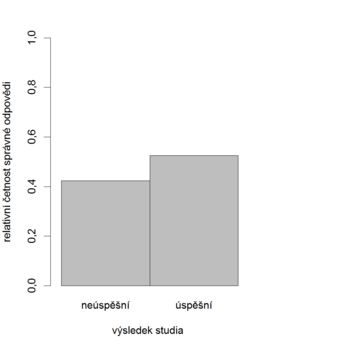
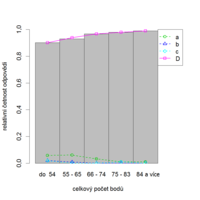
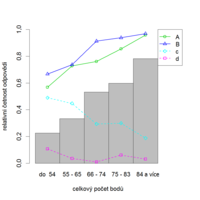
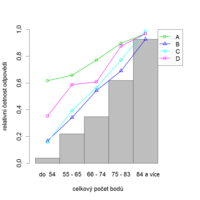
U správně zkonstruované položky by relativní četnost správné odpovědi měla růst s celkovým skóre (tj. celkovým počtem bodů), resp. měla by být vyšší pro úspěšné studenty než pro neúspěšné. Tedy čím lépe si studenti vedli v dané položce, tím lépe by si měli vést v celém testu nebo v nastávajícím studiu. Tak je tomu v následujícím příkladu (obr. 8.7a, 8.7b).
Graf: Grafické zobrazení vlastností položky
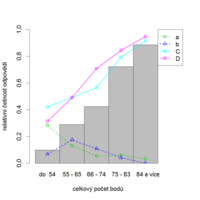
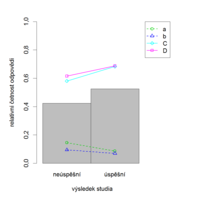
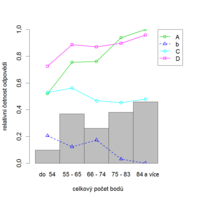
Pro přehlednost jsou v ukázkách správné odpovědi vyznačené velkými písmeny, distraktory jsou označeny písmeny malými. Pokud se jedná o položky s více nabízenými odpověďmi, je na místě vykreslit také relativní četnosti jednotlivých odpovědí (na následujících obrázcích jsou správné odpovědi zobrazeny plnou čarou a distraktory přerušovanou). Četnost volby distraktorů by měla být nižší u lepších studentů, přerušovaná čára by tedy měla mít klesající tendenci. Správné odpovědi by měli častěji volit lepší studenti, proto by čáry popisující správné odpovědi, stejně jako sloupcové grafy popisující celkovou úspěšnost v položce, měly také růst. Tak tomu je i v případě položky CH64 (obr. 8.8a, 8.8b).
|
Příklad snadné položky
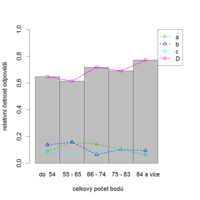
Jak je patrné i z grafického znázornění (obr. 8.9a, 8.9b), příliš snadné položky (stejně jako položky příliš těžké) mají nutně malou rozlišovací schopnost. Je to způsobeno skutečností, že na snadnou položku odpoví nesprávně jen velmi malé procento studentů, na velmi obtížnou položku zas odpoví jen velmi malé procento studentů správně.
V případě, že studenti volí pouze jedinou správnou/nejlepší odpověď, bude tato jediná plná čára korespondovat s vrcholky sloupcového grafu. Toto nastává jednak v případě, kdy studenti dopředu vědí, že se jedná o položky s jedinou nejlepší odpovědí (SBA), ale také v případě, kdy ze zadání položky s vícečetnou správnou odpovědí (např. MTF) sami vyvodí, že pouze jediná z nabízených variant může být správná. Tak tomu bylo i u položky CH10.
|
Příklad špatně rozlišující položky
Položka CH97 má také zřejmě jedinou správnou odpověď. Přestože její obtížnost je vyšší než u předchozí položky, i tato položka velice špatně rozlišuje mezi lepšími a slabšími studenty. Špatná rozlišovací schopnost této položky může být způsobena tím, že k dosažení správné odpovědi musí studenti provést správně hned několik úkonů a využít několika nezávislých znalostí a dovedností (znalost vzorce oxidu sírového, znalost atomové hmotnosti kyslíku, sestavení správné stechiometrické rovnice, správný výpočet), přičemž v každé z nich je možné udělat chybu.
|
Příklad málo validní položky
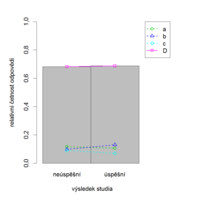
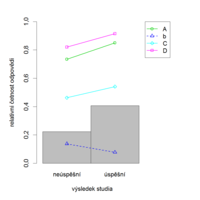
Položka CH55 má dvě správné odpovědi a dva distraktory, z nichž distraktor d je velice málo atraktivní. Stejně jako položka CH64 i CH55 velice dobře rozlišuje mezi studenty v testu úspěšnými a neúspěšnými, což je částečně dáno i její optimální obtížností. CH55 ale není příliš vhodná pro předpověď úspěšnosti ve studiu: neúspěšní studenti ji řešili dokonce o něco lépe než studenti úspěšní. Pro zvýšení validity testu bychom tuto položku měli z testu odebrat.
|
Příklad validní položky málo citlivé k celkovému výsledku v testu
CH28 je těžká položka, obzvláště s ohledem na těžko odhalitelnou správnou odpověď C. Dva správné názvy chemické sloučeniny respondenti patrně nečekali. Položka ovšem poměrně dobře rozlišuje mezi studenty úspěšnými a neúspěšnými ve studiu.
|
Příklad chybné položky
Obzvláště těžká je také položka CH44, kde distraktor d volí více studentů, než správnou odpověď A. Tu, zdá se, respondenti spíše hádali. Distraktor d dokonce volí studenti tím častěji, čím vyššího skóre v testu dosáhli. To budí podezření, že by položka mohla být chybná. Vskutku: správná odpověď je přibližně 0,008, v nabídnutých možnostech tedy chybí, avšak možnost d (autory testu označená jako nesprávná) se jí nejvíce blíží.
|
Příklad správně fungující položky
Výtečná diskriminační schopnost položky CH89 souvisí kromě optimální obtížnosti patrně také s faktem, že všechny nabízené odpovědi jsou správné. Zaškrtnout všechny nabízené odpovědi chce jistou dávku znalosti nebo odvahy.
|
Souhrnně jsou psychometrické vlastnosti zmíněných položek a příslušné závěry uvedeny v tabulce 8.3. Položky jsou v ní řazeny dle obtížnosti od nejsnazší úlohy. Shrneme-li doporučení pro položkovou analýzu, postup je následující:
V první řadě je potřeba odhadnout obtížnost položky, u příliš snadných ani příliš obtížných položek totiž nelze čekat rozumnou citlivost. U položek s více nabízenými odpověďmi je podobně potřeba zkontrolovat také relativní četnost volby jednotlivých distraktorů. O něco důležitější než obtížnost položek je pak jejich citlivost, tedy schopnost rozlišit mezi horšími a lepšími studenty (počítáno dle celkového výsledku v testu nebo dle jiného vnějšího kritéria). Nakonec se je potřeba podívat také na procento vynechaných odpovědí a zvážit, zda souvisí s obtížností položky nebo spíše s jejím pořadím v testu. Pokud je velké množství vynechaných odpovědí na konci testu, a zvláště pokud jejich obtížnost není příliš velká, je potřeba zvážit zkrácení testu.
| ID | obtížnost | Volba jednotlivých alternativ v % | citlivost podle skóre | citlivost podle úspěšnosti | % vynechaných | závěr slovy | |||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | ||||||
| CH10 | 0,95 | 4 | 1 | 1 | 95* | 0,10 | 0,02 | 0,0 | snadná položka, neatraktivní distraktory |
| CH97 | 0,68 | 11 | 11 | 8 | 68* | 0,13 | 0,00 | 2,4 | špatně rozlišující položka |
| CH55 | 0,49 | 77* | 84* | 35 | 5 | 0,49 | -0,07 | 0,2 | nevalidní položka, neatraktivní distraktor D |
| CH64 | 0,47 | 12 | 8 | 63* | 65* | 0,68 | 0,10 | 0,4 | správná položka |
| CH89 | 0,42 | 78* | 52* | 56* | 67* | 0,74 | 0,10 | 0,2 | správná položka |
| CH44 | 0,21 | 21* | 4 | 11 | 62 | -0,06 | -0,02 | 1,2 | podezřelá položka, distraktor D volen častěji než správná odpověď |
Pozn.: správná odpověď je označena *
Pokusme se nyní shrnout závěry, které lze z této položkové analýzy vyvodit:
- Žádná z analyzovaných položek nebyla vynechána více než 5 % respondentů. Z analyzovaných položek byla nejčastěji vynechána položka CH97 (2,7 % respondentů). Její umístění na konci testu nás může vést k zamyšlení, zda není časový interval příliš přísný, procento vynechaných odpovědí je ale malé.
- Položka CH10 je velice snadná, její distraktory jsou velmi neatraktivní a správnou odpověď volilo až 95 % studentů. Položka proto také špatně rozlišuje mezi lepšími a slabšími studenty, má téměř nulovou diskriminační schopnost.
- Neatraktivní jsou distraktory v položce CH97. Velice neatraktivní je také distraktor b v položce CH44. Naproti tomu distraktor d volilo v položce CH44 dokonce více respondentů než správnou odpověď A. Jak je vidět z odhadů citlivosti, položku řešili lepší studenti hůř než studenti slabší (kteří mohli správné řešení hádat). Tato položka je z tohoto důvodu velice podezřelá a jak by vyplynulo z revize textu, také nesprávně zadaná.
- Kromě zmíněné snadné položky CH10 a nesprávně zadané položky CH44, velice špatně mezi lepšími a slabšími studenty rozlišuje také položka CH97.
- Položka CH55 patří mezi položky, které mají uspokojivou citlivost vůči celkovému skóre, řešili ji ale lépe studenti ve studiu neúspěšní než studenti ve studiu úspěšní. Vynecháním této položky bychom mohli přispět ke zvýšení predikční validity celého testu.
- Položky CH64 a CH89 jsou příklady správně fungujících položek.
Shrneme-li, klasická položková analýza nám může pomoci rychle odhalit slabiny jednotlivých položek a nabízených odpovědí. Hlavní potíží klasických odhadů obtížnosti a citlivosti je jejich závislost na rozdělení znalosti u testovaných studentů. Zadáme-li položku několika skupinám studentů s různou úrovní znalosti, výsledný odhad obtížnosti (relativní četnost správné odpovědi) se může ve skupinách značně lišit. Podobně pokud odhadujeme citlivost položky u několika skupin s různou mírou homogenity, klasický odhad citlivosti se může ve skupinách značně lišit. S tímto nedostatkem se částečně vypořádává grafické hodnocení vlastností položky, kdy zobrazíme relativní četnost správných odpovědí v závislosti na celkovém počtu bodů – tj. v závislosti na jakési míře znalostí studenta. Při grafickém zobrazení již můžeme vnímat obtížnost jako relativní četnost správné odpovědi u skupiny s „průměrnou“ znalostí a citlivost jako sklon sloupcového grafu. To jsou hlavní myšlenky teorie odpovědi na položku, která nám takto obecněji pomůže vlastnosti položky také vyjádřit číselně.
Odkazy[upravit | editovat zdroj]
Reference[upravit | editovat zdroj]
- ↑ BYČKOVSKÝ, Petr a Karel ZVÁRA. Konstrukce a analýza testů pro přijímací řízení. 1. vydání. Praha : Univerzita Karlova v Praze, Pedagogická fakulta, 2007. 79 s. ISBN 978-80-7290-331-3.
- ↑ TAVAKOL, Mohsen a Reg DENNICK. Post Examination Analysis of Objective Tests. 1. vydání. AMEE, 2011. AMEE guide; sv. 54. ISBN 978-1-903934-91-3.