Harmonický oscilátor

Harmonický oscilátor je obecně jakýkoliv fyzikální systém, u kterého se fyzikální veličina charakterizující významnou fyzikální vlastnost daného systému mění v čase tak, že tyto změny jsou harmonickou funkcí (sinus, kosinus). Základním příkladem harmonického oscilátoru je těleso, které harmonicky kmitá kolem své rovnovážné polohy. Harmonický pohyb může být netlumený, amplituda harmonického pohybu v čase neklesá, nebo tlumený, kdy se projevuje disipace energie (působení "odporu prostředí") a amplituda harmonického pohybu v čase klesá.

Příklady harmonických oscilátorů mohou být např. těleso zavěšené na pružině, atom v molekule nebo třeba elektický LC oscilátor.

Základní pojmy

Harmonický pohyb je pohybem periodickým, je tedy charakterizovaný veličinami, které se v čase periodicky mění.

• Kmit je děj, v jehož průběhu se tyto veličiny vrátí k původním hodnotám.
• Perioda T ([T] = s) je doba, za kterou těžiště oscilátoru vykoná jeden kmit.
• Frekvence f ([f] = Hz = s^-1) je počet kmitů, které těžiště oscilátoru vykoná za jednotku času. Jedná se o převrácenou hodnotu periody.
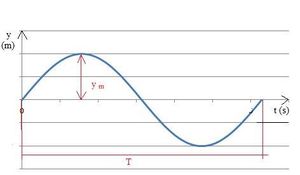
• Okamžitá výchylka (např. y ; [y] = m) je okamžitá vzdálenost těžiště oscilátoru od jeho rovnovážné polohy. Nabývá kladných i záporných hodnot. Diagram vyjadřující závislost této okamžité výchylky y na čase t se nazývá časový diagram a má tvar sinusoidy (viz obrázek). Funkce sinus a kosinus jsou v zásadě zaměnitelné, volba konkrétní z nich se řídí spíše zvyklostmi v dané oblasti.
• Amplituda (např. y_m ; [y_m] = m) je absolutní hodnota největší výchylky.

Kinematika harmonického pohybu

Časový diagram amplitudy harmonického pohybu.

Při harmonickém pohybu se okamžitá výchylka y mění s časem t podle funkce sinus (popř. kosinus). Tento děj popisuje rovnice harmonického pohybu:

$y(t)=y_{m}\sin \left(\omega t+\varphi _{0}\right)$

Parametr ω, [ω]=rad.s^-1 se nazývá úhlová frekvence kmitavého pohybu. Pro některé aplikace je vhodnější uvažovat úhlovou frekvenci a nikoliv frekvenci, i když spolu velmi úzce souvisí:

$\omega =2\pi f$

Parametr φ₀ se nazývá počáteční fáze kmitavého pohybu v čase t=0. Pokud v čase t=0 prochází oscilátor rovnovážnou polohou, pak φ₀=0.

Hodota φ = ωt + φ₀ se označuje jako fáze nebo též okamžitá fáze. Pro některé aplikace je výhodné fázi přepočítat postupným odečítáním případně přičítátním 2π přepočítat do intervalu od nuly do 2π. Při srovnávání dvou harmonických pohybů je zajímavý rozdíl fází, který se označuje jako jejich fázový posun nebo fázový rozdíl.

Okamžitou rychlost v kmitavého harmonického pohybu dostaneme derivací rovnice harmonického pohybu podle času:

$v(t)={\frac {\mathrm {d} }{\mathrm {d} t}}y(t)=\omega y_{m}\cos \left(\omega t+\varphi _{0}\right)$

Zřejmě pro maximální rychlost v_m platí:

$v_{m}=\omega y_{m}$

Okamžité zrychlení a kmitavého harmonického pohybu dostaneme derivací rovnice okamžité rychlosti podle času.

$a(t)={\frac {\mathrm {d} }{\mathrm {d} t}}v(t)=-\omega ^{2}y_{m}\sin \left(\omega t+\varphi _{0}\right)$

Dynamika harmonického pohybu

Dynamická podmínka harmonického pohybu

Harmonické kmitání mechanického oscilátoru je způsobeno silou F, jejíž velikost je přímo úměrná výchylce y a má v každém okamžiku směr do rovnovážné polohy:

$F=-\kappa y$

V případě, že je harmonickým oscilátorem myšleno těleso pohybující se na pružině, je konstanta úměrnosti totožná s tuhostí pružiny k, která je definována jako podíl síly F, která pružinu prodlouží o Δl:

$k={\frac {F}{\Delta l}}\;\;[Nm^{-1}]$

V případě, že uvažujeme jako harmonický oscilátor matematické kyvadlo nebo LC oscilátor, je fyzikální význam konstanty úměrnosti a ve druhém případě i "síly" poněkud složitější.

Přeměny energie v harmonickém oscilátoru

Konstantní mechanickou energii E harmonického oscilátoru můžeme určit v kterémkoli bodě trajektorie jako součet kinetické energie E_K a potenciální energie tělesa E_P v daném bodě. (Neuvažujeme disipativní síly, platí zákon zachování mechanické energie):

$E=E_{K}+E_{P}$

Potenciální energie

Potenciální energie tělesa hmotnosti m, které je připojeno k dokonalé pružině s tuhostí k a které je ve vzdálenosti x od rovnovážné polohy, je:

$E_{P}(x)={\frac {1}{2}}kx^{2}$

Kinetická energie

Rychlost harmonického pohybu je v okamžiku, kdy oscilátor dosáhne krajních poloh, nulová. V těchto bodech je tedy i kinetická energie nulová. Při průchodu rovnovážnou polohou je rychlost, a tedy i kinetická energie maximální. Platí vztah:

$E_{K}(x)={\frac {1}{2}}mv(x)^{2}$

Celková energie

Celkovou energii kmitavého pohybu v harmonickém oscilátoru lze snadno odvodit z výše uvedeného. Platí:

$E={\frac {1}{2}}mv_{m}^{2}$

Při harmonickém kmitavém pohybu se periodicky mění potenciální energie kmitání v energii kinetickou a naopak. Celková energie oscilátoru je konstantní.

Odkazy

Související články

• Osciloskop
• Tlumený harmonický oscilátor

Použitá literatura

• HOFMANN, Jaroslav. Fyzika I. 1. vydání. Praha : VŠCHT, 1998. ISBN 80-7080-314-2.

• TARÁBEK, Pavol a Petra ČERVINKOVÁ. Odmaturuj z fyziky. 2. vydání. Brno : Didaktis, 2006. ISBN 80-735-8058-6.

• LANK, Vladimír a Petra ČERVINKOVÁ. Fyzika v kostce. 3. vydání. Havlíčkův Brod : Fragment, 2004. ISBN 80-720-0968-0.

• LEPIL, Oldřich, Renata BEDNAŘÍK a Milan HÝBLOVÁ. Fyzika II. 3. vydání. Praha : Prometheus, 2006. ISBN 978-80-7196-185-7.