Měření závislosti, korelace a regrese
Statistické metody pro stanovení typu a síly závislosti mezi dvěma veličinami. V medicíně se tato metoda nejčastěji aplikuje při zkoumání vztahu onemocnění a jeho možných příčin.
Typ i sílu závislosti pro náhodný výběr rozsahu n můžeme orientačně posoudit z bodového grafu, v němž je každá dvojice dat (x, y) graficky znázorněna jedním bodem.
Typ závislosti určuje tvar křivky, kterou můžeme body proložit – lineární, exponenciální, logaritmická aj.
Regrese[upravit | editovat zdroj]
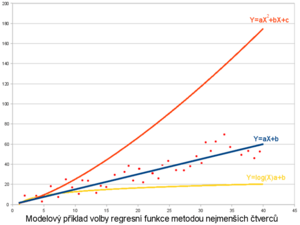
Při výběru regresní funkce se řídíme metodou nejmenších čtverců (viz lineární regrese), tzn. hledáme funkci, která leží nejblíže hodnotám námi zadaných dat a poté analyzujeme statistické vlastnosti přímky vybrané touto metodou.
Lineární regrese[upravit | editovat zdroj]
Lze použít je-li závislost veličiny y na x lineární.
V praxi: proložení bodů v grafu regresní přímkou y = a + bx tak, aby součet druhých mocnin odchylek jednotlivých bodů od přímky byl minimální (metoda nejmenších čtverců).
a, b = regresní koeficienty.
- a – posun na ose y (místo kde regresní přímka protíná svislou osu),
- b – sklon regresní přímky.
pozn. čtverec = druhá mocnina
Kvadratická regrese[upravit | editovat zdroj]
Speciální případ regrese lineární, kdy soubor dat proložíme kvadratickou funkcí (parabola) y = ax2 + bx + c.
a, b, c jsou regresní koeficienty, které můžeme v praxi odhadnout opět metodou nejmenších čtverců.
Logaritmická regrese[upravit | editovat zdroj]
Speciální případ regrese lineární, kdy soubor dat proložíme logaritmickou funkcí y = a + b·ln(x).
Síla statistické závislosti = korelace[upravit | editovat zdroj]
Vyjadřujeme ji různými vhodnými mírami, mezi které patří např. korelační koeficienty. Požadavek, aby absolutní hodnota míry statistické závislosti ležela v uzavřeném intervalu od 0 do 1. Statistická závislost však nemusí znamenat kauzalitu!
Pro měření síly závislosti se používá Pearsonův korelační koeficient ρ. Dle obecných platností nabývá hodnot −1 až +1. Je-li typ závislosti lineární, pak:
- nulová hodnota ρ – vyjadřuje lineární nezávislost veličin (Korelace nic neříká o funkční závislosti, ale jen o té lineární! Pouze u normálního rozdělení platí, že jsou-li veličiny lineárně nezávislé (nulová korelace), jsou zároveň funkčně nezávislé.),
- ρ > 0 – s rostoucími hodnotami jedné veličiny se zvyšují i hodnoty druhé (nebo obě klesají),
- ρ < 0 – s rostoucími hodnotami jedné veličiny klesají hodnoty druhé a naopak,
- krajní hodnoty +1 a −1 ukazují na funkční lineární závislost obou veličin.
Vysoký stupeň závislosti (korelace) často odráží příčinný vztah, ale nemusí tomu tak být vždy.
Někdy nemáme jasně určeno, která veličina je nezávislá a která závislá. Lineární regrese X na Y nedává stejnou regresní přímku jako regrese Y na X. Druhá mocnina korelačního koeficientu se nazývá koeficient determinace a jeho hodnota měří velikost lineární vztahu mezi X a Y bez ohledu na to, která veličina je závislá a která nezávislá – tento koeficient získaný z obou regresí je stejný.
Z grafu lineární regrese lze usuzovat na hodnotu ρ – čím je úhel, který svírají obě regresní přímky (vyjadřující závislost x na y a y na x) menší, tím větší je absolutní hodnota ρ.
Korelační studie[upravit | editovat zdroj]
K posuzování vlivu třetích faktorů se využívá výpočtu parciálních korelačních koeficientů, které jsou stanoveny pro jednotlivé dvojice znaků, jejichž asociace se zkoumá (např. v souboru, kde je zaznamenáván věk, tlak krve a hladina cholesterolu v krvi se stanoví korelační koeficienty pro vztahy: r1 – pro vztah věk a tlak, r2 – pro vztah věk a chol., r3 – pro vztah chol. a tlak). Tak lze vypočítat parciální koeficient např. pro vztah hladiny cholesterolu a TK při eliminaci věku jako třetího faktoru a po otestování statistické významnosti potvrdit nebo nepotvrdit asociaci mezi těmito znaky.
Odkazy[upravit | editovat zdroj]
Související články[upravit | editovat zdroj]
Externí odkazy[upravit | editovat zdroj]
Použitá literatura[upravit | editovat zdroj]
- MACHEK, Josef a Jiří LIKEŠ. Matematická statistika. 2. vydání. Praha : SNTL, 1988. ISBN 1. Jiří Likeš, Josef Machek, Matematická statistika, SNTL Praha 1988, s. 165-169.
- ZVÁROVÁ, Jana. Biomedicínská statistika I. : Základy statistiky pro biomedicínské obory [online] . dotisk 1 vydání. Praha : Karolinum, 1998. 218 s. Dostupné také z <http://www.euromise.cz/education/textbooks.html>. ISBN 80-7184-786-0.
- BENCKO, Vladimír, et al. Epidemiologie, výukové texty pro studenty 1. LFUK, Praha. 2. vydání. Praha : Univerzita Karlova v Praze – Nakladatelství Karolinum, 2002. 168 s. s. 78-80. ISBN 80-246-0383-7.