Pufry

Kyselost vnitřního prostředí v lidském organismu se udržuje ve velmi úzkém rozmezí hodnot pH. Je tomu tak proto, že na pH závisí vlastnosti bílkovin i dalších molekul. Dojde-li k výraznější změně pH, podstatně se změní například rychlosti enzymových reakcí, vlastnosti receptorů, transportérů a iontových kanálů atd. Lidský organismus přitom čelí řadě vlivů, které by mohly pH jeho vnitřního prostředí vychýlit. Jde jak o působení látek, které přijímáme jako potravu nebo se kterými přichází do kontaktu naše pokožka, tak i o produkci kyselin a zásad metabolickými pochody.

Na udržování pH prostředí se podílejí pufry (též nárazníky, tlumivé roztoky, ústojné roztoky).

Pufr je většinou učebnic definován jako konjugovaný pár kyseliny (nebo zásady), který je schopný udržovat v jistém rozmezí stabilní pH i po přidání silné kyseliny či zásady do systému. Konjugovaným párem chápeme kyselinu (resp. zásadu) a její sůl, která se vytvoří po přidání zásady (resp. kyseliny) do systému. Jedná se o dvojici látek, které přecházejí jedna ve druhou příjmem/ztrátou jednoho protonu. Pokud se jedná o silnou kyselinu (resp. zásadu), je (téměř) kompletně rozdisociovaná, a tedy případné reakce se zúčastní všechny dostupné částice (např. pufr HCl-KCl, rozdisociované na H⁺, Cl^- a K⁺). Daleko častěji se používají slabé kyseliny, jejichž nerozdisociované části (např. CH₃COOH) představují zásobní pool, k jehož rozštěpení (na CH₃COO^- a H⁺) dojde po přidání látky o jiném pH.

Přesný výpočet teoretického pH je velmi komplikovaný (nutno vzít v úvahu teplotu, koncentraci jednotlivých složek pufrů, aktivitní koeficienty, rozpouštědlo, iontovou sílu sytému aj.). Proto se častěji pH systémů měří experimentálně. Nejjednodušším odhadu pH pufru je Hendersonova-Hasselbalchova rovnice (dále v textu označovaná jako H.-H. rce). Lze ji odvodit zlogaritmováním rovnice (1) pro rovnovážnou konstantu:

(1)

$K_{a}={\frac {[{\mbox{H}}^{+}]\cdot [{\mbox{A}}^{-}]}{[{\mbox{HA}}]}}$, resp. $K_{b}={\frac {[{\mbox{B}}^{+}]\cdot [{\mbox{OH}}^{-}]}{[{\mbox{BOH}}]}}$,

kde HA (resp. BOH) představuje kyselinu (bázi), A^- (B⁺) anion kyseliny (či kation báze), a hranaté závorky molární koncentraci. Uvedená rovnice je nepřesná, neboť místo koncentrací je třeba brát do výpočtu aktivity. Pro kyselinu a její sůl zjednodušeně platí rovnice (2):

(2)

$pH=pK_{a}+\log {\frac {[{\mbox{A}}^{-}]}{[{\mbox{HA}}]}}$;

podobně pro zásadu a její sůl rovnice (3):

(3)

$pOH=pK_{b}+\log {\frac {[{\mbox{B}}^{+}]}{[{\mbox{BOH}}]}}$, tedy $pH=14-pK_{b}-\log {\frac {[{\mbox{B}}^{+}]}{[{\mbox{BOH}}]}}$.

Složení pufrů je více či méně komplikované a podřizuje se především účelům, pro které má být zvolený systém užit. Optimální oblast aktivity zvoleného pufru je dána jeho složením. Z jednodušších lze zmínit pufr Clark–Lube (HCl+KCl) pH 1,1–2,2; citrátový pH 2,2–3,6; fosfátový (NaH₂PO₄ + Na₂HPO₄, používaný pro oblast pH krve) – pH 5,8–8,0. Avšak existují a používají se též pufry vícesložkové, jejichž oblast účinnosti pokrývá prakticky celou škálu pH, např. Brittonův–Robinsonův, jehož účinná oblast aktivity se pohybuje v rozmezí pH od 1,8 do téměř 12.

Počet molů jednosytné kyseliny a soli v pufru a přídavku jednosytné kyseliny přidané k pufru vypočteme podle rovnic (4):

(4)

$n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}=[{\mbox{A}}^{-}]\cdot V_{\text{pufr}}$;     $n_{\text{kyselina}}=[{\mbox{HA}}]\cdot V_{\text{pufr}}$;     $n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}=[{\mbox{H}}^{+}]\cdot V_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}$

Pro výpočet teoretické hodnoty pH pufrů tvořených slabou kyselinou a její solí po přídavku kyseliny lze v prvním přiblížení užít vztah (5a) odvozený z H.-H. rce (2).

(5a)

$pH=pK_{a}+\log {\frac {n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}-n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}{n_{\text{kyselina}}+n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}}$

a po přídavku zásady ke stejnému systému pak rovnici (5b):

(5b)

$pH=pK_{a}+\log {\frac {n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}+n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}{n_{\text{kyselina}}-n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}}$

kde index „pufr“ se vztahuje k objemům před přidáním kyseliny (resp. zásady), „sůl“ k soli obsažené v pufru, „kyselina“ ke kyselině v pufru a „přídavek" jen k hodnotám samotného přídavku před smísením s pufrem.

Pro slabou zásadu a její sůl se užívá analogický vztah odvozený z rovnice (3).

Nejjednodušší výpočty je možné provádět pro uni-univalentní systémy, tj. za předpokladu, kdy pufr je tvořen jednosytnou slabou kyselinou a její solí (např. CH₃COOH/CH₃COONa, NaH₂PO₄/Na₂HPO₄) a přidávána je též jednosytná zásada či kyselina (např. HCl či NaOH).

Teoretická hodnota pH pufru se často liší od experimentálně zjištěné (ať již vlivem neidealit či úmyslně zanedbaných faktorů při jejich výpočtu (iontová síla, teplota, rozpouštědlo aj.)). Často se proto pufry připravují dvojstupňově: nejdříve se smísí složky ve vypočteném (tabelovaném) poměru tak, aby výsledek odpovídal požadované hodnotě pH, následně se jeho skutečná hodnota pH změří pomocí správně zkalibrovaného pH-metru a dostatečně přesná hodnota se dosáhne odpovídajícími přídavky kyseliny či zásady (po každém přídavku nutno systém řádně promíchat, nechat vyrovnat teplotu a hodnotu přístroje odečítat až po ustálení).

Množství látky, jejíž přídavek lze vykompenzovat pomocí pufru, určuje tzv. pufrační kapacita β. Je určena především složením a koncentrací pufru. Čím je koncentrace složek pufru vyšší, tím je tlumivá schopnost též vyšší (např. pro úzké rozmezí pufrů a malé očekávané přídavky látek lze použít málo koncentrovaný pufr a naopak). Pufrační kapacita klesá se zředěním pufru. Největší kapacitu mají pufry složené ze slabých kyselin a jejich solí (resp. slabých zásad a jejich solí) o stejné látkové koncentraci, tedy přesněji, u nichž je pH = pK. To lze odvodit z rovnice (2) a (3), kde při rovnosti koncentrací soli kyseliny (resp. zásady) je log(1/1) = 0 a pH = pKa (resp. pH = 14 − pK_b). Při jiných poměrech se mění dle logaritmu poměru koncentrací jednotlivých složek. Obecně se v literatuře uvádí, že „jednoduchý“ pufr, složený ze dvou složek, je použitelný v rozmezí pH od (pK_a − 1) do (pK_a + 1) (tzn., že poměr kyseliny a soli se pohybuje v poměru od 10:1 po 1:10).

Zjednodušený, empirický výpočet pufrační kapacity β se provádí dle následující rovnice (6):

(6)

$\beta ={\frac {dc_{b}}{dpH}}\approx {\frac {\Delta c_{b}}{\Delta pH}}=-{\frac {\Delta c_{a}}{\Delta pH}}$,

kde „d“ označuje derivaci (čteno „dé cé podle dé péHá“), Δc_a změnu molární koncentrace kyseliny, Δc_b změnu molární koncentrace zásady, ΔpH změnu pH dosaženou přídavkem kyseliny Δc_a či zásady Δc_b.

Přesnější vztah umožňující výpočet β získáme diferenciální úpravou H.-H. rce (tzv. van Slykeho rovnice – čtěte „fan Slykeho“) (rce (7a)):

(7a)

$\beta =2,3\cdot \left([{\mbox{H}}^{+}]+[{\mbox{OH}}^{-}]+{\frac {K_{a}\cdot c_{a}\cdot [{\mbox{H}}^{+}]}{([{\mbox{H}}^{+}]+K_{a})^{2}}}\right)\approx 2,3\cdot c_{a}\cdot {\frac {K_{a}\cdot [{\mbox{H}}^{+}]}{(K_{a}+[{\mbox{H}}^{+}])^{2}}}=2,3\cdot [{\mbox{A}}^{-}]\cdot \left(1-{\frac {[{\mbox{A}}^{-}]}{c_{a}}}\right)$

kde c_a značí celkovou koncentraci pufru (součet molárních koncentrací složek pufru), tj. c_a = [HA] + [A^-], a K_a disociační konstantu (kyselé složky) pufračního systému (konstanta 2,3 je přibližná a zajišťuje přepočet přirozeného a dekadického logaritmu).

Analogická rovnice (7b) platí pro tlumivou kapacitu směsí slabých zásad a konjugovaných kyselin:

(7b)

$\beta =2,3\cdot \left([{\mbox{H}}^{+}]+[{\mbox{OH}}^{-}]+{\frac {K_{b}\cdot c_{b}\cdot [{\mbox{OH}}^{-}]}{([{\mbox{OH}}^{-}]+K_{b})^{2}}}\right)\approx 2,3\cdot c_{b}\cdot {\frac {K_{b}\cdot [{\mbox{OH}}^{-}]}{(K_{b}+[{\mbox{OH}}^{-}])^{2}}}$

První část rovnice zahrnuje i tlumivé kapacity silných elektrolytů (silné kyseliny a silné zásady), zatímco zjednodušený vzorec je užíván pro přibližný výpočet tlumivé kapacity pufrů, vytvořených od slabých kyselin typu HA. Pro výpočet pufrační kapacity se často používá i vztah (7c), který vzniká jednoduchou úpravou vztahu (7a):

(7c)

$\beta =2,3\cdot [{\mbox{A}}^{-}]\cdot \left(1-{\frac {[{\mbox{A}}^{-}]}{c_{a}}}\right)$

Příprava pufru

Při přípravě pufrů se vychází buď z roztoků slabých kyselin, resp. bazí a jejich solí, nebo z pevných solí vícesytných kyselin nebo jejich roztoků, anebo se částečně neutralizuje slabá kyselina, resp. báze silnou bazí, resp. kyselinou.

Připravíme-li pufr přesně podle návodu a změříme jeho pH, nemusí pH vždy úplně odpovídat teoreticky spočítané hodnotě. Zvlášť u koncentrovanějších roztoků totiž bývá aktivita vodíkových iontů nižší než jejich koncentrace. Navážky jednotlivých složek pro přípravu nejběžnějších pufrů lze najít v tabulkách.

Titrace octanového pufru

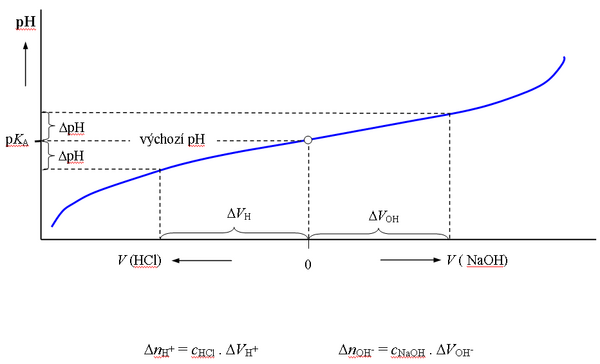
Grafickým vyjádřením Hendersonovy-Hasselbachovy rovnice je titrační křivka slabé kyseliny nebo zásady. Při titraci pufru, tzn. při postupném přidávání zředěných roztoků silné kyseliny nebo zásady k roztoku pufru se pH zpočátku mění jen pozvolna, po překročení hodnoty pH = K_A ± 1 jsou změny již značné. Z průběhu titrační křivky pufru dané koncentrace (c_HB + cn_B) lze určit pufrační kapacitu pro kteroukoliv hodnotu pH.

Smícháním stejných objemů roztoků octové kyseliny a octanu sodného o stejné látkové koncentraci vzniká pufr s poměrem složek 1:1, jehož pH je rovno pK_A octové kyseliny (4,75).