Kompartmenty

Kompartment je homogenní matematickou veličinou. Představuje zjednodušený model skutečnosti, sloužící ke znázornění dějů. Mohou být malé, nebo velké, avšak vždy se jedná o abstraktní jednotky. Mezi typické kompartmenty se řadí plazma (eventuálně i krev), intracelulární a extracelulární tekutina, tuková tkáň apod. Navzájem jsou odděleny membránami. Jako systém se popisuje soubor kompartmentů, mezi kterými se vyměňuje látka.

Modely kompartmentů

Modely kompartmentů jsou základem farmakokinetické analýzy dat. Jsou závislé na koncentraci látky c a čase t. Pro zjednodušení se využívají jedno-, dvou- a tříkompartmentové modely.

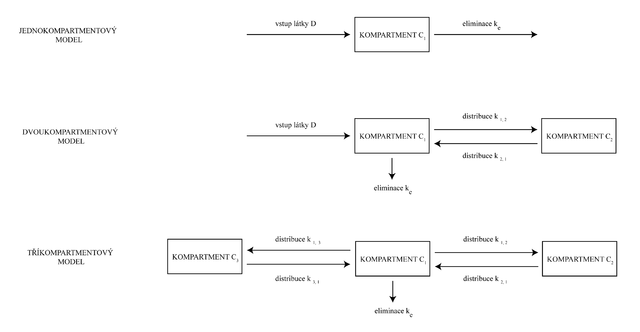
Jednokompartmentový model

Tento typ modelu je nejjednodušší. Celé tělo je zde považováno za jediný kompartment. Předpokládá se, že po aplikaci je látka v systému rychle a stejnoměrně rozptýlena. Z tohoto důvodu je nemožné přesně znázornit distribuci látky v organismu. Význam má tento typ modelu při popisu a predikci pohybu léčiva např. při opakovaném podání.

Pro účely analýzy dat je nejvýhodnější pracovat s koncentrací. Množství látky D₁ (látka v kompartmentu) je děleno jednotkou objemu (distribuční objem).

C₀ = D₀/V_d

C₀ = koncentrace látky v čase t = 0;
D₀ = množství látky v t = 0;
V_d = distribuční objem.

Upravenou rovnici pro jednokompartmentový model lze vyjádřit takto:

C=C₀ × e^–kt^[1]

C = koncentrace v čase t;
C₀ = počáteční koncentrace;
k = eliminační konstanta;
e = Eulerovo číslo.

Uvedená rovnice popisuje snižující se koncentraci podané látky v kompartmentu. Pokles je způsoben pouze eliminací látky.

Dvoukompartmentový model

Některé látky nemohou být okamžitě rozptýleny v celém objemu těla. Pro simulaci této skutečnosti se využívá systému dvou kompartmentů. První je centrální a druhý je periferní. Předpokládáme výměnu látky mezi kompartmenty za účelem udržení rovnováhy.

Diferenciální rovnice pro centrální kompartment:

dC₁/dt = −C₁×(k_e + k_1,2) + C₂ × k_2,1

Diferenciální rovnice pro periferní kompartment:

dC₂/dt = C₁ × k_1,2 − C₂ × k_2,1

k_1,2, k_2,1 = rychlostní konstanty, které udávají množství látky, vyměňující se za jednotku času

Předchozí dvě rovnice lze sloučit do jedné:

C_t = Ae^−αt + Be^−βt^[1]

Ae^−αt = distribuční fáze;
Be^−βt = eliminační fáze;
α,β = sklon křivky během distribuční a eliminační fáze.

V tomto případě je úbytek látky v centrálním kompartmentu závislý na míře eliminace a množství, které se vymění s druhým kompartmentem.

Tříkompartmentový a multikompartmentový model

S vzrůstajícím množstvím kompartmentů nabývá systém na komplexnosti.

Tříkompartmentový systém se skládá z centrálního kompartmentu a dvou periferních. Centrální je lépe prokrvený než druhé dva.

dC₁/dt = –C₁ × (k_e + k_1,2 + k_1,3) + C₂ × k_2,1 + C₃ × k_3,1

Odkazy

Reference

↑ ^a ^b BURTIS, Carl A, Edward R ASHWOOD a David E BRUNS. Tietz textbook of clinical chemistry and molecular diagnostics. 4. vydání. St. Louis, Mo : Elsevier Saunders, 2006. 2412 s. s. 1241. ISBN 978-0-7216-0189-2.

Externí odkazy

Multi-compartment model - (anglicky)

Zdroje

BURTIS, Carl A, Edward R ASHWOOD a David E BRUNS. Tietz textbook of clinical chemistry and molecular diagnostics. 4. vydání. St. Louis, Mo : Elsevier Saunders, 2006. 2412 s. s. 1237-1247. ISBN 978-0-7216-0189-2.

DIPIRO, Joseph T, et al. Concepts in Clinical Pharmacokinetics. 5th Edition vydání. 2010. 250 s. s. 1-9. ISBN 978-1-58528-241-8.

Farmakokinetická analýza - Katedra farmakologie a toxikologie UK

[clinical_biochemistry-1] BURTIS, Carl A, Edward R ASHWOOD a David E BRUNS. Tietz textbook of clinical chemistry and molecular diagnostics. 4. vydání. St. Louis, Mo : Elsevier Saunders, 2006. 2412 s. s. 1241. ISBN 978-0-7216-0189-2.

[1]