Radioaktivita (2. LF UK)

Tento článek pojednává o praktickém cvičení z biofyziky 2. LF UK. Pokud se chcete dozvědět něco více o obecné teorii radioaktivity, klikněte sem.

Zadání[upravit | editovat zdroj]

Ověřte platnost teoretických vztahů pro pokles intenzity radioaktivního záření pomocí stínění různými materiály a pokles intenzity radioaktivního záření se vzdálenosti od zdroje.
Ověřte pomocí Poissonova rozdělení stochastickou podstatu přeměn γ a β.

Teoretický základ[upravit | editovat zdroj]

Radioaktivita je jaderný děj, při kterém se nestabilní mateřský radionuklid samovolně mění na stabilnější (opět radioaktivní) nebo stabilní dceřiný nuklid, který má optimálnější poměr protonů a neutronů v jádře. Účelem radioaktivní přeměny je dosažení stability atomu. Tento děj je charakteristický tím, že současně dochází k emisi částic, kvanta elektromagnetického záření nebo zachycení elektronu z elektronového obalu za vzniku ionizujícího záření.

Proces radioaktivní přeměny se opakuje, dokud není nové jádro stabilní; následně se jeho struktura již samovolně nemění. Protože jde o procesy probíhající v jádře atomu, není možné rychlost proměny jádra ovlivnit žádným fyzikálním nebo chemickým procesem. Podle rozdílného chování záření v elektrickém a magnetickém poli rozlišujeme záření α, β a γ.

Historie radioaktivity[upravit | editovat zdroj]

Za objevitele radioaktivity je považován Henri Becquerel, francouzský fyzik a člen francouzské Akademie věd, který se z počátku zabýval optickými vlastnostmi látek. Po objevu rentgenových vln německý fyzikem W. C. Roentgenem v roce 1895 se začal soustředit na vztah mezi rentgenovým zářením a fluorescencí, přičemž při zkoumaní fluorescence uranových solí narazil na dosud nepopsaný jev - přirozenou radioaktivitu. Při pokusech s fotografickou deskou a materiálem, který na fotografické desce způsoboval chemické reakce bez nutnosti světelného ozáření, usoudil, že soli vyzařují záření jiné než světelné povahy. Výsledky těchto pokusů zveřejnil v roce 1896.

Na jeho objevy navázali manželé Pierre Curie a Marie Curie-Skłodowska. Ti ještě v roce 1896 objevili podobné vlastnosti u sloučenin thoria. Marie Curie-Skłodowska vůbec poprvé pojmenovala tuto vlastnost, do této doby známou jako Becquerelovy paprsky, jako radioaktivitu. Po zkoumaní a měření dalších hornin manželé Curieovi objevili řadu dalších radioaktivních prvků. Mezi ně se řadí polonium (150krát radioaktivnější než uran) a radium (900krát radioaktivnější než uran). V roce 1899 doplnila Marie Curie-Skłodowska své objevy o hypotézu, že radioaktivita je přirozený děj, při kterém jádra atomů těžkých prvků vyzařují záření a zároveň se přeměňují na jádra lehčích prvků. Tento jev byl označen přirozená radioaktivita. Oba manželé získali spolu s Henri Becquerelem v roce 1903 Nobelovu cenu.

Pojem umělá radioaktivita zavedli v roce 1934 manželé Frédéric a Iréne Joliot-Curieovi. Tento jev popsali na základě experimentů s ostřelováním hliníku částicemi alfa, během kterých vznikal nový nuklid fosforu a neutron. Za své pokusy získali v roce 1935 Nobelovu cenu.

Objev radioaktivity změnil celosvětový pohled na atom, který byl do té doby brán jako nezničitelný a neměnný.

Zákony radioaktivních přeměn[upravit | editovat zdroj]

V radioaktivním nuklidu, vyzařujícím alfa nebo beta záření, probíhají procesy přeměn, díky kterým vzniká stabilní nuklid. Tyto lze charakterizovat podle aktivity A, měrné nebo objemové aktivity či podle poločasu přeměny T_1/2.

Aktivitou A se vyjadřuje počet radioaktivních přeměn za jednu sekundu. Měření probíhá v jednotkách becquerel [Bq]. Jedna přeměna za sekundu odpovídá 1 Bq. Dříve byla používána jednotka curie [Ci], 1Ci odpovídá 3,7*10¹⁰ Bq.

Zákon radioaktivní přeměny lze matematicky formulovat takto:

„Aktivita je přímo úměrná celkovému počtu dosud nepřeměněných jader s přeměnovou konstantou.“

$A(t)=\lambda \,N(t)$

N odpovídá počtu atomů ve vzorku v určitém čase t a λ je přeměnová konstanta.

Zákon se může vyjádřit ještě dalšími dvěma způsoby:

a) v exponenciálním tvaru

$N=N_{0}e^{-\lambda t}$ ,

kde N₀ = počet atomů v čase t = 0

b) v diferenciálním stavu

$-{\frac {dN(t)}{dt}}=\lambda \,N(t)$

Z aktivity A lze vyjádřit měrnou (hmotnostní) aktivitu, která se rovná aktivitě 1 kg zářiče a objemovou (popř. plošnou) aktivitu, která odpovídá aktivitě jednoho krychlového (popř. čtverečného) metru zářiče.

Jako poločas přeměny T_1/2 označujeme dobu, během které klesne aktivita vzorku na polovinu. Od objevu radioaktivity bylo v přírodě zjištěno 50 přirozených radionuklidů. Jejich poločasy nabývají rozdílných hodnot v řádech sekund až miliard roků. Je tedy jasné, že v přírodě mohou být jen takové radionuklidy, které mají velmi dlouhý poločas, nebo takové, které v přírodě neustále vznikají.

Přeměnová konstanta λ je charakteristická pro jednotlivé radioaktivní jádro a vyjadřuje pravděpodobnost jaderné přeměny. Tato konstanta odpovídá úměrnosti mezi počtem přeměněných radioaktivních jader a celkovým počtem nepřeměněných.

Lze ji vyjádřit takto:

$\lambda \ ={\frac {\ln 2}{T_{1/2}}}$

Radioaktivní přeměna je zcela náhodná, není možné s přesností určit okamžik přeměny, lze určit pouze pravděpodobnost dané přeměny. Přeměny jsou spontánní bez vnějšího zásahu.

Druhy ionizujícího záření[upravit | editovat zdroj]

Záření α[upravit | editovat zdroj]

Záření α je proud letících jader helia tzv. α-částic. Částice alfa je tvořena dvěma protony a dvěma neutrony, je tedy kladně nabitá s elektrickým nábojem o hodnotě +2e a má nenulovou klidovou hmotnost.

Záření α vzniká radioaktivní přeměnou izotopů těžkého prvku, kdy dochází k emisi částice α' a uvolnění 'energie odpovídající hmotnostnímu úbytku v systému.

Nuklid vzniklý rozpadem α má z důvodu zachování nukleonového čísla a elektrického náboje protonové číslo o 2 nižší, je tedy v periodické soustavě prvků posunut vzhledem k původnímu jádru o dvě místa vlevo. Ve srovnání s hmotností emitujícího jádra má emitovaná částice velmi malou hmotnost. Kinetická energie jádra při emisi částice je prakticky zanedbatelná. Samo jádro těžkého prvku se vrací z excitovaného stavu do stavu energeticky základního emisí kvant záření γ. Proto je běžné, že tento typ radioaktivní přeměny je zářením gama doprovázen.

Záření alfa má silné ionizační účinky, má však malou pronikavost. Rychlost šíření dosahuje až 10⁷m.s^-1 a letící částice proniká jen několikacentimetrovou vrstvou vzduchu. Odstínit se dá i běžným listem papíru. Vnější působení na člověka nemá prakticky žádný účinek, neboť je záření pohlceno buňkami dlaždicového kožního epitelu. Vnitřní působení záření (např. v plicích) však může poškodit genetický materiál a tak vést ke vzniku nádorového onemocnění. Alfa záření lze využít také k léčebným účelům. Jeho působení v určitých dávkách aktivuje obranné mechanismy buněk.

Mezi látky, které jsou zdroji záření α patří například uran, radium nebo radon.

Záření β[upravit | editovat zdroj]

Záření β je druh přirozeného izobarického rozpadu radionuklidů, při němž zůstává nezměněn počet nukleonů v jádře. Z jader prvků s nadbytkem neutronů jsou však vyzářeny částice nesoucí buď kladný elektrický náboj, tzv. pozitony (β+), nebo částice nesoucí záporně nabitý elektrický náboj, tedy elektrony (β-). Při tomto procesu je navíc emitována ještě další částice, tzv. antineutrino (v), která v sobě odnáší rozdíl mezi energií uvolněnou jádrem a kinetickou energií. Záření β je asi stokrát pronikavější než záření α, nicméně má menší ionizační účinky. Může proniknout pouze materiály s nízkou hustotou, popř. materiály s malou tloušťkou (zachytí jej i hliníková fólie). Vzhledem k tomu, že se jedná o elektricky nabité částice, vychyluje se toto záření v elektrickém i magnetickém poli.

• β+: Při vyzáření proudu pozitronů prvkem se uvnitř původního jádra přemění proton na neutron. Díky tomu má nově vzniklý prvek protonové číslo o 1 jednotku menší než původní atom, v PSP dochází k posunu prvku o jedno místo vlevo.

• β-: Při vyzáření proudu elektronů prvkem se uvnitř původního jádra přemění neutron na proton. Nově vzniklému prvku se protonové číslo zväčší o 1 jednotku od původního atomu, tudíž se prvek v PSP posouvá o jedno místo vpravo.

Záření γ[upravit | editovat zdroj]

Záření γ je na rozdíl od předchozích dvou přeměn elektromagnetickým zářením. Má nejkratší vlnové délky (pod 125-200 pm), extrémně vysoké frekvence vlnění (vyšší než 10¹⁹ Hz) a nejvyšší energii (nad 100 keV). Má výrazný kvantový ráz, takže se projevuje jako proud částic (fotonů). Fotony se uvolňují z jader přeskupováním nukleonů v radionuklidu.

Energie nukleonů v jádře je kvantována, každý nukleon se vyskytuje jen v určitém kvantovém stavu. Přechod z jednoho stavu do druhého se může dít pouze za současného dodání nebo uvolnění energie. Při záření γ tedy nedochází k přeměně prvků, ale pouze ke snížení vnitřní energie nukleonů v jádře. Vznikne jádro v excitovaném stavu a nadbytečné energie se zbaví vyzářením jednoho nebo několika fotonů záření γ.

Vzhledem k velice krátkým vlnovým délkám má záření γ velkou energii a velkou pronikavost. Magnetické pole průběh tohoto záření nijak neovlivňuje, poněvadž je nehmotné. Záření γ zpravidla doprovází α i β záření.

Přírodní radiační pozadí[upravit | editovat zdroj]

Přírodní radiační pozadí (nazýváno také jako přírodní radioaktivita) lze charakterizovat jako ionizující záření z vesmíru i naší Země. Hodnota tohoto pozadí je závislá na místních podmínkách, s časem se ale výrazně nemění. Samotné záření má náhodný charakter a pro konkrétní místa na povrchu Země nabývá konkrétních hodnot, které se od sebe mohu vzájemně velmi lišit, a to i více než stonásobně, což je dáno především rozdílným obsahem radioaktivních izotopů v půdě, výskytem radioaktivních zdrojů vytvořených uměle člověkem a také různou nadmořskou výškou.

Na současnou úroveň přírodního radiačního pozadí je příroda spolu se všemi organismy včetně člověka dobře přizpůsobena. Navíc je lidský organismus schopen se postupně na vyšší hodnotu přírodního pozadí během života adaptovat.

Přírodní radiační pozadí je tedy způsobeno zejména: - rozpady nestabilních jader radioaktivních izotopů v zemské kůře, příp. v jejím horním plášti - kosmickým zářením a jeho interakcí se zemskou atmosférou

Ochrana před ionizujícím zářením[upravit | editovat zdroj]

Vzhledem k možným negativním účinkům ionizujícího záření na lidský organismus se v praxi využívá tří základních principů pro ochranu před tímto zářením: ochrana časem, ochrana vzdáleností a ochrana stíněním. Častá je i jejich kombinace.

Více o ochraně před ionizujícím záření naleznete zde.

Ochrana stíněním[upravit | editovat zdroj]

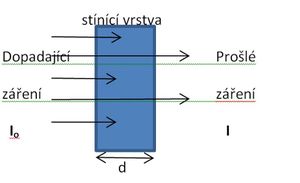
Princip ochrany stíněním před účinky radioaktivního (ionizujícího) záření spočívá v použití překážky z určitého materiálu, která se umístí mezi zdroj záření a předpokládané místo výskytu chráněných osob. Částice ionizujícího záření poměrně snadno prochází vzduchem. Pokud se však těmto částicím nastaví do cesty nějaká překážka z materiálu hustšího, než je vzduch, překážka bude tyto částice pohlcovat (dojde k jejich vzájemné interakci), a to v míře závislé na tloušťce překážky a její hustotě. Překážka o větší tloušťce i hustotě (vyšším protonovém čísle) odstíní záření lépe.

Množství pohlceného (odstíněného) a množství prošlého záření lze popsat exponenciálním vztahem I = I_o . e ^-u^{. d}(platí pro rovnoběžný svazek záření), kde I je intenzita prošlého záření, I_o je výchozí intenzita záření, d je tlouštka překážky a u je lineární součinitel zeslabení. Intenzita prošlého záření I tedy klesá exponenciálně s rostoucí tloušťkou stínící vrstvy d. Místo lineárního součinitele zeslabení používá údaj tzv. polotloušťky (d_1/2) absorbce, což je taková tloušťka vrstvy daného materiálu, která zeslabí intenzitu daného záření na polovinu.

Zeslabení intenzity záření absorbční (stínící) vrstvou tloušťky d se pomocí polotloušťky d_1/2dá vyjádřit jednoduchým vztahem I / I_o = 2 ^-d/(d1/2), kde I je intenzita prošlého záření, I_o je výchozí intenzita záření, d je tloušťka stínění a d_1/2 je polotlouštka absorpce. Z tohoto vztahu můžeme již jednoduše spočítat pro určitou požadovanou konkrétní hodnotu zeslabení záření celkovou tloušťku vrstvy stínění z konkrétního materiálu.

Následující tabulka uvádí pro určité hodnoty zeslabení záření gama vypočítané hodnoty tloušťky vybraných materiálů.

**tloušťka vrstvy stínění (mm) pro materiál**
hodnota zeslabení I/Io pro záření o energii E = 200 [keV]	beton	olovo
50% ( = polotloušťka)	21	1,4
10%	70	4,7
1%	140	9,3
0,1%	210	14,0

Z hodnot např. vyplývá, že na hodnotu zeslabení záření na 10 % je třeba stínění o tloušťce odpovídající přibližně 3,3 polotloušťkám, na hodnotu zeslabení záření na 1 % je třeba stínění o tloušťce odpovídající přibližně 7 polotloušťkám a na hodnotu zeslabení záření na 0,1 % je třeba stínění o tloušťce odpovídající přibližně 10 polotloušťkám (vše počítáno pro hodnotu energie záření E = 200 keV).

Pozn.:Z výše uvedeného vztahu I = I_o . e ^{- u}^{. d} by se mohlo zdát, že záření nelze úplně odstínit, neboť základní vlastností exponenciální funkce se záporným exponentem je, že se blíží nule až v nekonečnu. Ve skutečnosti však každý zářič emituje jen konečný počet kvant. Po průchodu dostatečnou tloušťkou (desítkami či stovkami polotlouštěk d_1/2) dojde v praxi vždy nakonec k pohlcení i posledního kvanta.

Praktické využití[upravit | editovat zdroj]

Pro ochranu stíněním v praktickém využití musíme identifikovat převládající typ radiačního záření. Správnou ochranou lze významně eliminovat nebezpečí radiačního záření. Důležité uplatnění těchto opatření nalézáme v energetice, stavebnictví a medicíně.

Pro gama záření je třeba použít prvků s vysokou hustotou a vysokým protonovým číslem, nejčastěji olovo (Pb). Typickým příkladem jsou olověné kontejnery pro skladování a transport gama zářičů či olověné cihly. Ze stavebních materiálů je vhodný zejména beton s příměsí barytu (obklopující jaderný reaktor), dále ocel, wolfram či magnetit. Tyto materiály se přidávají do exteriérových omítek a barev. V medicíně jsou důležité především olověné zástěny odstiňující záření z rentgenového přístroje. Olověný obal nemusí být nikterak robustní - pro odstínění záření stačí obvykle několikamilimetrová, maximálně několikacentimetrová vrstva (záleží na materiálu, intenzitě a povaze záření). To je dokladem další vlastnosti jmenovaných materiálů - mají relativně nízké hodnoty polotloušťky.

Záření typu beta je v porovnání se zářením gama slabší a méně pronikavé, tudíž je i ochrana před ním snazší a méně nákladná. Nejčastěji je tvořena plexisklem, hliníkovou fólií či plastem. Důležitým faktem je, že kvůli vzniku tzv. brzdného záření nemůžeme pro ochranu před zářením beta použít jako stínič olovo.

Záření alfa lze pro svoji malou pronikavost a rychlost snadno odstínit pouhým papírem.

Praktické úkoly[upravit | editovat zdroj]

Souprava Gamabeta[upravit | editovat zdroj]

Pro praktické úlohy budete používat školní soupravu se zářičem Gamabeta. Souprava obsahuje stínící destičky z hliníku, železa, cínu, mědi a olova. Typ záření, které bude přístroj vysílat, nastavíte natočením červené značky na krytu zářiče proti písmenu G nebo B. Parametry následně vysílaného záření naleznete v tabulce.

Písmeno	Typ záření	Nuklid	Poločas rozpadu nuklidu
G	gama	²⁴¹Am	432,7 let
B	beta	⁹⁰Sr	29,1 let

Čítač impulzů propojte kabelem s indikátorem záření (světle šedý obdélník se zářezem), oba přístroje zapněte. Na indikátor nenasazujte výměnnou absorpční destičku (kovový hranol; používá se při měření záření s vysokou aktivitou).

Úkol č. 1: Měření radiačního pozadí[upravit | editovat zdroj]

Jelikož se přirozená radioaktivita vyskytuje v malé míře všude kolem nás, zjišťuje se hodnota tohoto pozadí v okolí zdroje záření, aby bylo při měření hodnot detekovaných částic pocházejících ze zdroje dosaženo přesnějšího výsledku.

Měření se provádí 10x po 100 sekundách, bez použití zdroje záření, který umístěte co nejdále od detektoru (ven z místnosti), aby bylo měření přesnější. Z naměřených hodnot se vypočítá průměrná hodnota radiačního pozadí po dobu 100 s, z níž se poté určí výsledná hodnota pro desetisekundový interval.

Úkol č. 2: Ochrana stíněním[upravit | editovat zdroj]

Měření se provádí 5x po 10 sekundách pro 3 různé kovové absorpční destičky (Al, Cu, Fe), zářič je umístěn 4 cm od detektoru. První série měření je pro záření β a druhá pro záření γ. Druh záření měníme pootočením hlavy zářiče tak, aby byl symbol daného záření na straně zářiče s otvorem.

Úkol č. 3: Ochrana vzdáleností[upravit | editovat zdroj]

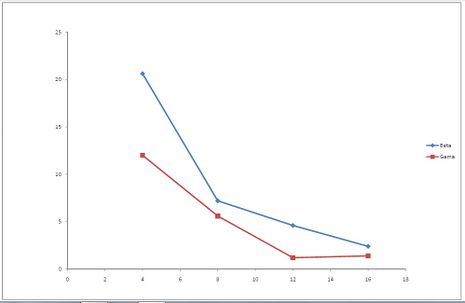
Měření se provádí 5x po 10 sekundách pro 4 zadané vzdálenosti - jednou pro záření β a podruhé pro záření γ. Tedy - pětkrát změříme dané záření ve vzdálenosti 4 cm, pětkrát ve vzdálenosti 8 cm a tak dále. Poté pootočíme hlavou zářiče a změříme stejně tak druhé záření. Od získaných hodnot se odečítá hodnota radiačního pozadí, aby došlo k minimalizaci chyby měření. Výsledkem tohoto úkolu je graf a vaše závěry. Graf buď podpoříte teorií, nebo ho teorií popřete a vysvětlíte, proč neodpovídá teoretickým poznatkům.

U úkolů 2 a 3 nezapomeňte zdroj v drážce zajistit zarážkou, jinak mohou být naměřené hodnoty nepřesné.

Graf znázorňující pokles závislosti počtu detekovaných částic radioaktivního záření na vzdálenosti zářiče od detektoru záření

Úkol č. 4: Poissonovo rozdělení[upravit | editovat zdroj]

Toto rozdělení pravděpodobnosti, pojmenované podle francouzského matematika S. D. Poissona, mají náhodné proměnné, které popisují četnosti jevů s těmito vlastnostmi:

pravděpodobnost je úměrná velikosti intervalu (lambda pro polovinu intervalu bude poloviční)
pravděpodobnost, že se v jednom okamžiku (na jednom místě) vyskytnou dvě události je zanedbatelná
pravděpodobnost se nemění v různých stejně velkých intervalech
pravděpodobnosti událostí v různých intervalech jsou nezávislé

(Důležité jsou zejména poslední dva předpoklady. Pokud jsou porušeny, přinášejí dodatkový rozptyl (overdispersion) a snadno poznáme, že znak už nemá Poissonovo rozdělení)
pak pravděpodobnostní rozdělení počtu výskytů jevu v určitém časovém intervalu se nazývá Poissonovo rozdělení a má hustotu pravděpodobnosti p(x)=(λ^x/x!)*e^-λ
v daném jednotkovém úseku, λ > 0 je parametr,X =0, 1, 2,...

Poissonovo rozdělení značíme P(λ);

jeho střední hodnota i rozptyl (průměrný počet výskytů zkoumaného jevu v daném úseku jednotkové délky) je rovna konstantě λ
Dále platí, že výskyt sledovaného jevu záleží pouze na délce intervalu t a nikoli na jeho počátku ani na tom, kolikrát jev nastoupil před jeho počátkem. Tomu se říká, že Poissonovo rozdělení nemá paměť.

X = počet výskytů dané náhodné události za jednotku času
Pokud bychom však opakovali měření vždy pro stejný časový interval délky T, naměřili bychom různé počty pulzů X. Důvodem je statistický charakter radioaktivity. Přitom některé konkrétní počty X naměříme vícekrát než jiné. Pravděpodobnosti, že za dobu měření T naměříme určitý počet pulzů X, se vzájemně liší! Matematická statistika však umí tyto pravděpodobnosti určit, předpovědět (mluvíme o rozdělení pravděpodobnosti) Např. regulérní hrací kostka má rovnoměrné rozdělení pravděpodobnosti, tedy jakékoliv z čísel 1 až 6 musí padnout se stejnou pravděpodobností.

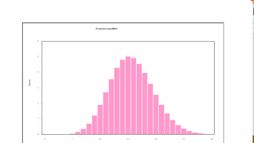
Když máme k dispozici velký počet měření detekce částic ze zářiče (v tomto případě 50 měření po 10 sekundách pro jeden typ záření, když zářič bude 4 cm od detektoru), můžeme sestavit graf četnosti jednotlivých hodnot. Jedná se o „Histogram“ - prosté vyhodnocení, která hodnota byla kolikrát zaznamenána.

Histogram, četnost počtu detekovaných částic vždy za období 10 s

Automaticky se vypočítá průměr naměřených hodnot - tzv. střední hodnota a, podle které se vypracuje graf teoretického rozložení hodnot. Stručně řečeno: průměrný počet zaznamenaných impulsů (detekovaných částic) má v ideálním stavu nejvyšší četnost, směrem k menšímu i většímu počtu impulsů se četnost postupně snižuje.

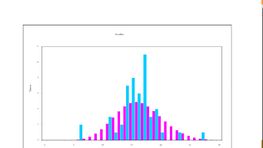
Ideální průběh Poissonova rozložení pravděpodobnosti

Získané grafy se poté spojí do jednoho, takže lze zkorigovat chybu způsobenou malým počtem měření. Nastavení korekce se provede tak, aby Poissonova křivka lépe doplňovala experimentálně naměřené hodnoty. Naměřené hodnoty nejvyšší četnosti by měly co nejlépe odpovídat „vrcholu křivky“. Doplněná hodnota „a“ je zvoleným průměrem hodnot, který posune ideální obraz grafu do reálné situace daného měření.

Prolnutí histogramu a ideálního poissonova roložení, je ještě nutná korekce

Prolnutí naměřených hodnot s ideálním Poissonovým rozložením po korekci

Empirická pravidla pro volbu Poissonova rozdělení Poissonovo rozdělení použijeme, když

rozptyl je přibližně roven průměru,
průměr je menší než 10,
histogram údajů je zešikmen (zešikmení mizí s rostoucím průměrem, nad 10 už je histogram téměř symetrický)

Protokol[upravit | editovat zdroj]

V diskuzi popište teoretickou závislost poklesu intenzity radioaktivního záření v závislosti na vzdálenosti a teoretickou závislost poklesu intenzity stíněním různými materiály. U stínění radioaktivního záření popište, které druhy ionizující záření jsou absorbovány více nebo méně a které materiály obecně více nebo méně absorbují ionizující záření. Nakonec porovnejte získané výsledky s uvedenými teoretickými předpoklady.

V závěru zhodnoťte zda získané průběhy poklesu intenzity radioaktivního záření odpovídají teoretickým předpokladům.

Video[upravit | editovat zdroj]

Zdroje[upravit | editovat zdroj]

ROSINA, Jozef. Biofyzika : pro zdravotnické a biomedicínské obory. 1. vydání. Praha : Grada, 2013. ISBN 978-80-247-4237-3.

SVOBODA, Emanuel, et al. Přehled středoškolské fyziky. 4. vydání. Praha : Prometheus, 2008. 0 s. ISBN 9788071963073.

AMLER, E, et al. Praktické úlohy z biofyziky I. 1. vydání. Praha : Ústav biofyziky UK, 2. lékařské fakulty, 2006.

LUSTIG, F. a P. BROM. Závislost radioaktivity na druhu a tlouštce vrstvy stínicího materiálu [online]. [cit. 2014-12-16]. <http://kdt-38.karlov.mff.cuni.cz/shielding/theory.html>.

ŠVUB, M.. Poissonovo rozložení pravděpodobnosti [online]. [cit. 2014-12-16]. <https://is.muni.cz/th/rhxzm/poissonovo_rozlozeni_svub.pdf?so=nx>.

ČEZ, A.S.,. Poznávej bez obav ionizující záření: souprava Gamabeta 2007 [online]. [cit. 2015-11-30]. <https://www.cez.cz/edee/content/file/pro-media-2014/05-kveten/gamabeta_letak.pdf>.

BROKLOVÁ, Zdeňka. Učíme jadernou fyziku. [online]. [cit. 2012-02-29]. Dostupné z: https://www.cez.cz/cs/vyzkum-a-vzdelavani/pro-studenty/materialy-ke-studiu/tiskoviny/11.html
DUFKOVÁ, Marie. Domácí pokusy z jaderné fyziky. [online]. [cit. 2012-02-29]. Dostupné z: https://www.cez.cz/cs/vyzkum-a-vzdelavani/pro-studenty/materialy-ke-studiu/tiskoviny/9.html
Vypracovaný protokol z měření 2014/2015
Břetislav Fajmon, UMAT FEKT, VUT Brno Poissonovo a exponenciální rozdělení pravděpodobnosti

Související stránky[upravit | editovat zdroj]

Portál:Biofyzikální praktikum (2. LF UK)