Pufry, pufrační kapacita, oxidoredukce, elektrodové děje (1. LF UK, VL)

Tento text slouží jako studijní materiál pro předmět Lékařská chemie a biochemie 1. LF UK

Pufry (ústojné roztoky, tlumivé roztoky)

[ ✎ upravit vložený článek ]

Kyselost vnitřního prostředí v lidském organismu se udržuje ve velmi úzkém rozmezí hodnot pH. Je tomu tak proto, že na pH závisí vlastnosti bílkovin i dalších molekul. Dojde-li k výraznější změně pH, podstatně se změní například rychlosti enzymových reakcí, vlastnosti receptorů, transportérů a iontových kanálů atd. Lidský organismus přitom čelí řadě vlivů, které by mohly pH jeho vnitřního prostředí vychýlit. Jde jak o působení látek, které přijímáme jako potravu nebo se kterými přichází do kontaktu naše pokožka, tak i o produkci kyselin a zásad metabolickými pochody.

Na udržování pH prostředí se podílejí pufry (též nárazníky, tlumivé roztoky, ústojné roztoky).

Pufr je většinou učebnic definován jako konjugovaný pár kyseliny (nebo zásady), který je schopný udržovat v jistém rozmezí stabilní pH i po přidání silné kyseliny či zásady do systému. Konjugovaným párem chápeme kyselinu (resp. zásadu) a její sůl, která se vytvoří po přidání zásady (resp. kyseliny) do systému. Jedná se o dvojici látek, které přecházejí jedna ve druhou příjmem/ztrátou jednoho protonu. Pokud se jedná o silnou kyselinu (resp. zásadu), je (téměř) kompletně rozdisociovaná, a tedy případné reakce se zúčastní všechny dostupné částice (např. pufr HCl-KCl, rozdisociované na H⁺, Cl^- a K⁺). Daleko častěji se používají slabé kyseliny, jejichž nerozdisociované části (např. CH₃COOH) představují zásobní pool, k jehož rozštěpení (na CH₃COO^- a H⁺) dojde po přidání látky o jiném pH.

Přesný výpočet teoretického pH je velmi komplikovaný (nutno vzít v úvahu teplotu, koncentraci jednotlivých složek pufrů, aktivitní koeficienty, rozpouštědlo, iontovou sílu sytému aj.). Proto se častěji pH systémů měří experimentálně. Nejjednodušším odhadu pH pufru je Hendersonova-Hasselbalchova rovnice (dále v textu označovaná jako H.-H. rce). Lze ji odvodit zlogaritmováním rovnice (1) pro rovnovážnou konstantu:

(1)

$K_{a}={\frac {[{\mbox{H}}^{+}]\cdot [{\mbox{A}}^{-}]}{[{\mbox{HA}}]}}$, resp. $K_{b}={\frac {[{\mbox{B}}^{+}]\cdot [{\mbox{OH}}^{-}]}{[{\mbox{BOH}}]}}$,

kde HA (resp. BOH) představuje kyselinu (bázi), A^- (B⁺) anion kyseliny (či kation báze), a hranaté závorky molární koncentraci. Uvedená rovnice je nepřesná, neboť místo koncentrací je třeba brát do výpočtu aktivity. Pro kyselinu a její sůl zjednodušeně platí rovnice (2):

(2)

$pH=pK_{a}+\log {\frac {[{\mbox{A}}^{-}]}{[{\mbox{HA}}]}}$;

podobně pro zásadu a její sůl rovnice (3):

(3)

$pOH=pK_{b}+\log {\frac {[{\mbox{B}}^{+}]}{[{\mbox{BOH}}]}}$, tedy $pH=14-pK_{b}-\log {\frac {[{\mbox{B}}^{+}]}{[{\mbox{BOH}}]}}$.

Složení pufrů je více či méně komplikované a podřizuje se především účelům, pro které má být zvolený systém užit. Optimální oblast aktivity zvoleného pufru je dána jeho složením. Z jednodušších lze zmínit pufr Clark–Lube (HCl+KCl) pH 1,1–2,2; citrátový pH 2,2–3,6; fosfátový (NaH₂PO₄ + Na₂HPO₄, používaný pro oblast pH krve) – pH 5,8–8,0. Avšak existují a používají se též pufry vícesložkové, jejichž oblast účinnosti pokrývá prakticky celou škálu pH, např. Brittonův–Robinsonův, jehož účinná oblast aktivity se pohybuje v rozmezí pH od 1,8 do téměř 12.

Počet molů jednosytné kyseliny a soli v pufru a přídavku jednosytné kyseliny přidané k pufru vypočteme podle rovnic (4):

(4)

$n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}=[{\mbox{A}}^{-}]\cdot V_{\text{pufr}}$;     $n_{\text{kyselina}}=[{\mbox{HA}}]\cdot V_{\text{pufr}}$;     $n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}=[{\mbox{H}}^{+}]\cdot V_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}$

Pro výpočet teoretické hodnoty pH pufrů tvořených slabou kyselinou a její solí po přídavku kyseliny lze v prvním přiblížení užít vztah (5a) odvozený z H.-H. rce (2).

(5a)

$pH=pK_{a}+\log {\frac {n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}-n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}{n_{\text{kyselina}}+n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}}$

a po přídavku zásady ke stejnému systému pak rovnici (5b):

(5b)

$pH=pK_{a}+\log {\frac {n_{{\text{s}}^{\circ }\!\!\!{\text{ul}}}+n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}{n_{\text{kyselina}}-n_{{\text{p}}{\check {\text{r}}}{\acute {\iota }}{\text{davek}}}}}$

kde index „pufr“ se vztahuje k objemům před přidáním kyseliny (resp. zásady), „sůl“ k soli obsažené v pufru, „kyselina“ ke kyselině v pufru a „přídavek" jen k hodnotám samotného přídavku před smísením s pufrem.

Pro slabou zásadu a její sůl se užívá analogický vztah odvozený z rovnice (3).

Nejjednodušší výpočty je možné provádět pro uni-univalentní systémy, tj. za předpokladu, kdy pufr je tvořen jednosytnou slabou kyselinou a její solí (např. CH₃COOH/CH₃COONa, NaH₂PO₄/Na₂HPO₄) a přidávána je též jednosytná zásada či kyselina (např. HCl či NaOH).

Teoretická hodnota pH pufru se často liší od experimentálně zjištěné (ať již vlivem neidealit či úmyslně zanedbaných faktorů při jejich výpočtu (iontová síla, teplota, rozpouštědlo aj.)). Často se proto pufry připravují dvojstupňově: nejdříve se smísí složky ve vypočteném (tabelovaném) poměru tak, aby výsledek odpovídal požadované hodnotě pH, následně se jeho skutečná hodnota pH změří pomocí správně zkalibrovaného pH-metru a dostatečně přesná hodnota se dosáhne odpovídajícími přídavky kyseliny či zásady (po každém přídavku nutno systém řádně promíchat, nechat vyrovnat teplotu a hodnotu přístroje odečítat až po ustálení).

Množství látky, jejíž přídavek lze vykompenzovat pomocí pufru, určuje tzv. pufrační kapacita β. Je určena především složením a koncentrací pufru. Čím je koncentrace složek pufru vyšší, tím je tlumivá schopnost též vyšší (např. pro úzké rozmezí pufrů a malé očekávané přídavky látek lze použít málo koncentrovaný pufr a naopak). Pufrační kapacita klesá se zředěním pufru. Největší kapacitu mají pufry složené ze slabých kyselin a jejich solí (resp. slabých zásad a jejich solí) o stejné látkové koncentraci, tedy přesněji, u nichž je pH = pK. To lze odvodit z rovnice (2) a (3), kde při rovnosti koncentrací soli kyseliny (resp. zásady) je log(1/1) = 0 a pH = pKa (resp. pH = 14 − pK_b). Při jiných poměrech se mění dle logaritmu poměru koncentrací jednotlivých složek. Obecně se v literatuře uvádí, že „jednoduchý“ pufr, složený ze dvou složek, je použitelný v rozmezí pH od (pK_a − 1) do (pK_a + 1) (tzn., že poměr kyseliny a soli se pohybuje v poměru od 10:1 po 1:10).

Zjednodušený, empirický výpočet pufrační kapacity β se provádí dle následující rovnice (6):

(6)

$\beta ={\frac {dc_{b}}{dpH}}\approx {\frac {\Delta c_{b}}{\Delta pH}}=-{\frac {\Delta c_{a}}{\Delta pH}}$,

kde „d“ označuje derivaci (čteno „dé cé podle dé péHá“), Δc_a změnu molární koncentrace kyseliny, Δc_b změnu molární koncentrace zásady, ΔpH změnu pH dosaženou přídavkem kyseliny Δc_a či zásady Δc_b.

Přesnější vztah umožňující výpočet β získáme diferenciální úpravou H.-H. rce (tzv. van Slykeho rovnice – čtěte „fan Slykeho“) (rce (7a)):

(7a)

$\beta =2,3\cdot \left([{\mbox{H}}^{+}]+[{\mbox{OH}}^{-}]+{\frac {K_{a}\cdot c_{a}\cdot [{\mbox{H}}^{+}]}{([{\mbox{H}}^{+}]+K_{a})^{2}}}\right)\approx 2,3\cdot c_{a}\cdot {\frac {K_{a}\cdot [{\mbox{H}}^{+}]}{(K_{a}+[{\mbox{H}}^{+}])^{2}}}=2,3\cdot [{\mbox{A}}^{-}]\cdot \left(1-{\frac {[{\mbox{A}}^{-}]}{c_{a}}}\right)$

kde c_a značí celkovou koncentraci pufru (součet molárních koncentrací složek pufru), tj. c_a = [HA] + [A^-], a K_a disociační konstantu (kyselé složky) pufračního systému (konstanta 2,3 je přibližná a zajišťuje přepočet přirozeného a dekadického logaritmu).

Analogická rovnice (7b) platí pro tlumivou kapacitu směsí slabých zásad a konjugovaných kyselin:

(7b)

$\beta =2,3\cdot \left([{\mbox{H}}^{+}]+[{\mbox{OH}}^{-}]+{\frac {K_{b}\cdot c_{b}\cdot [{\mbox{OH}}^{-}]}{([{\mbox{OH}}^{-}]+K_{b})^{2}}}\right)\approx 2,3\cdot c_{b}\cdot {\frac {K_{b}\cdot [{\mbox{OH}}^{-}]}{(K_{b}+[{\mbox{OH}}^{-}])^{2}}}$

První část rovnice zahrnuje i tlumivé kapacity silných elektrolytů (silné kyseliny a silné zásady), zatímco zjednodušený vzorec je užíván pro přibližný výpočet tlumivé kapacity pufrů, vytvořených od slabých kyselin typu HA. Pro výpočet pufrační kapacity se často používá i vztah (7c), který vzniká jednoduchou úpravou vztahu (7a):

(7c)

$\beta =2,3\cdot [{\mbox{A}}^{-}]\cdot \left(1-{\frac {[{\mbox{A}}^{-}]}{c_{a}}}\right)$

Příprava pufru

Při přípravě pufrů se vychází buď z roztoků slabých kyselin, resp. bazí a jejich solí, nebo z pevných solí vícesytných kyselin nebo jejich roztoků, anebo se částečně neutralizuje slabá kyselina, resp. báze silnou bazí, resp. kyselinou.

Připravíme-li pufr přesně podle návodu a změříme jeho pH, nemusí pH vždy úplně odpovídat teoreticky spočítané hodnotě. Zvlášť u koncentrovanějších roztoků totiž bývá aktivita vodíkových iontů nižší než jejich koncentrace. Navážky jednotlivých složek pro přípravu nejběžnějších pufrů lze najít v tabulkách.

Titrace octanového pufru

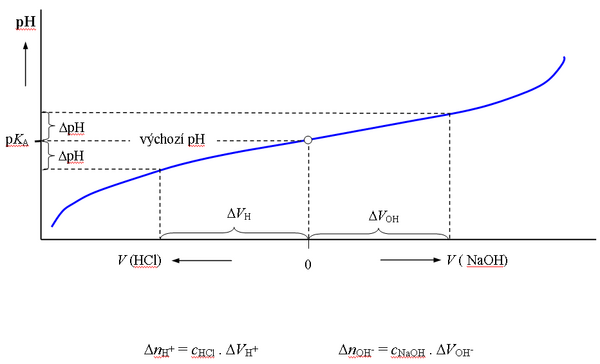
Grafickým vyjádřením Hendersonovy-Hasselbachovy rovnice je titrační křivka slabé kyseliny nebo zásady. Při titraci pufru, tzn. při postupném přidávání zředěných roztoků silné kyseliny nebo zásady k roztoku pufru se pH zpočátku mění jen pozvolna, po překročení hodnoty pH = K_A ± 1 jsou změny již značné. Z průběhu titrační křivky pufru dané koncentrace (c_HB + cn_B) lze určit pufrační kapacitu pro kteroukoliv hodnotu pH.

Smícháním stejných objemů roztoků octové kyseliny a octanu sodného o stejné látkové koncentraci vzniká pufr s poměrem složek 1:1, jehož pH je rovno pK_A octové kyseliny (4,75).

Elektrochemie

Elektrochemické metody můžeme rozdělit do dvou velkých skupin. První tvoří metody založené na oxidačně-redukčních dějích, které probíhají na kovových elektrodách. Využívají elektrochemických článků, které jsou buď v rovnováze (potenciometrie), nebo jimi protéká elektrický proud a soustava se v čase mění (voltametrie, coulometrie). Druhou skupinu elektrochemických technik tvoří metody, při nichž se měří jiné elektrické vlastnosti látek – např. vodivost (konduktometrie), impedance a kapacita.

Elektrodové děje

[ ✎ upravit vložený článek ]

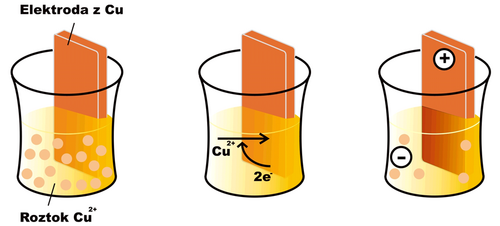
Ponoříme-li do roztoku kovového iontu (např. Cu²⁺) elektrodu ze stejného kovu (v daném případě mědi), začne na povrchu elektrody probíhat oxido-redukční reakce

Cu²⁺ + 2 e⁻ $\rightleftharpoons$ Cu

V případě mědi je za běžných podmínek rovnováha uvedené reakce posunuta poněkud doprava (u jiných látek, např. zinku, tomu může být opačně). Na povrchu elektrody se ukládá vrstvička vyredukované mědi a elektroda posupně získává kladný náboj, protože se z ní odčerpávají volné elektrony. Roztok, do nějž je elektroda ponořena, naopak získává záporný náboj, neboť z něj bez náhrady ubývají kationty Cu²⁺. Po určité době se reakce zastaví, neboť elektrostatické síly dalšímu přesunu nabitých částic brání, a ustaví se rovnováha charakterizovaná jistým elektrickým potenciálem na elektrodě. Snahu elektrody přijímat nebo odevzdávat elektrony charakterizuje tzv. redukční potenciál (E_red). Pokud mají všechny složky elektrodové reakce aktivitu rovnou jedné, nebo se nacházejí v podobě, na niž je standardní stav vztažen (např. pevné skupenství), mluvíme o standardním redukčním potenciálu (E⁰_red).

Potenciál vzniklý výše popsaným způsobem na jedné elektrodě nedokážeme změřit přímo. Můžeme však vytvořit článek složený ze dvou různých elektrod – např. kovů (obecně poločlánků) a dvou odpovídajících elektrolytů. Příkladem může být tzv. Daniellův článek: Cu v roztoku Cu²⁺ a Zn v roztoku Zn²⁺. Podle toho, jestli mají jednotlivé kovy tendenci být spíš v oxidované nebo redukované podobě, je můžeme uspořádat do tzv. Beketovovy elektrochemické řady (K, Ca, Al, Zn, Fe, Ni, Pb, H, Bi, Cu, Hg, Ag, Au). Pro tyto účely se za nulu považuje elektrodový potenciál tzv. standardní vodíkové elektrody. Kovy, které mají záporný standardní redukční potenciál a tedy snadno odevzdávají elektron, jsou v řadě nalevo od vodíku (tj. draslík má snahu se oxidovat na K⁺). Ionty kovů, které jsou vpravo, naopak elektrony snadno přijímají (např. Ag⁺ se snadno redukuje na Ag) a jejich standardní redukční potenciál je kladný.

Výše zmíněný Daniellův článek se schematicky zapisuje Zn | Zn²⁺ || Cu²⁺ | Cu (negativnější kov se zapisuje vlevo). Na zinkové elektrodě probíhá redoxní reakce

Zn²⁺ + 2 e⁻ $\rightleftharpoons$ Zn,

která má rovnovážnou konstantu K_Zn a je charakterizovaná standardním redukčním potenciálem E⁰_red(Zn); na měděné elektrodě probíhá výše uvedená reakce

Cu²⁺ + 2 e⁻ $\rightleftharpoons$ Cu

s rovnovážnou konstantou K_Cu a standardním redukčním potenciálem E⁰_red(Cu). V daném případě platí, že K_Cu > K_Zn, resp. E⁰_red(Cu) > E⁰_red(Zn). Jinými slovy měď se bude redukovat a ukládat na elektrodě ochotněji, než zinek. Z měděné elektrody se tak spotřebuje více elektronů, než ze zinkové. V konečném důsledku bude mít měděná elektroda vůči zinkové kladné napětí, které můžeme změřit.

Necháme-li mezi elektrodami protékat proud, budou se „scházející" elektrony do měděné elektrody dodávat ze zinkové a výsledný děj bude možné zapsat takto:

Zn → Zn²⁺ + 2e⁻

Cu²⁺ + 2e⁻ → Cu

Vodičem mezi elektrodami i solným můstkem poteče proud tak dlouho, dokud se nerozpustí zinková elektroda, nebo (což je pravděpodobnější) dokud se nespotřebuje Cu²⁺ z elektrolytu, popřípadě se druhý elektrolyt nenasytí ionty Zn²⁺ (vybití elektrochemického článku).

Napětí článku je rovno rozdílu potenciálu obou elektrod. Článek, na němž probíhají děje samovolně, spontánně („produkuje“ napětí) nazýváme článkem galvanickým (ΔG < 0). Pokud na něj napětí vkládáme a děje jsou „vynuceny“ vloženým napětím (ΔG > 0), nazýváme takovýto článek elektrolytickým.

Popsané elektrodové děje jsou poměrně obecné a obdobným způsobem probíhají v nejrůznějších soustavách složených z různých kovů a iontů.

 Podrobnější informace naleznete na stránce elektrochemický potenciál.

.

pH-metrie

[ ✎ upravit vložený článek ]

Pravděpodobně největšího věhlasu se dostalo elektrochemii díky možnosti měřit pH prostřednictvím tzv. skleněné elektrody. I v tomto případě měříme potenciál mezi dvěma poločlánky, tj. měrnou (indikační) a referntní elektrodou. V praxi bývá referentní elektroda často zabudovaná do jednoho těla společně s měrnou elektrodou – mluvíme o kombinované pH-metrické elektrodě.

Na rozdíl od výše popsaných elektrochemických článků, kde vzniká napětí v důsledku propojení různých kovů (redukce a oxidace), u skleněné elektrody je napětí produkováno v důsledku výměnných dějů. Ty probíhají mezi ionty „usazenými“ v krystalové mřížce skla (membráně) a ionty v roztoku. Na poměrně pravidelné křemičitanové krystalové mřížce skla jsou elektrostatickými silami vázány ionty, především vodíku a alkalických kovů (např. sodíku). Při styku s roztokem se na povrchu vytváří solvatovaná vrstvička, ve které dochází k výměně iontů alkalických kovů (např. sodíkových) a vodíkových iontů mezi roztokem a sklem.

 Podrobnější informace naleznete na stránce Skleněná elektroda.

Pro skleněnou vodíkovou elektrodu platí rovnice (9):

(9)

$E=konst+{\frac {RT}{F}}\cdot \ln(a_{H^{+}}+K_{S}\cdot a_{Na^{+}})\;{\dot {=}}\;konst+{\frac {RT}{F}}\cdot \ln a_{H^{+}}=konst.-2,3\cdot pH$

kde K_s je konstanta selektivity, která ukazuje, jak selektivně elektroda reaguje na jeden nebo druhý iont. Při její dostatečně nízké hodnotě lze zanedbat člen rovnice (9), který ji obsahuje, a použít zjednodušený tvar. Výraz „konst.“ zahrnuje standardní redukční potenciál, způsob přípravy elektrody, druh a složení skla, kvalitu povrchu, „stáří“ i vnitřní náplň elektrody. Pro zjednodušení se používá u většiny přístrojů dekadický logaritmus a proměnné se shrnou do jedné „konstantní“ číselné hodnoty 2,3 (pro teplotu 25 °C).

Při konstantním potenciálu referentní elektrody je měřené napětí přímo úměrné pH analyzovaného roztoku ve velké části celého rozsahu možných pH. Ve skutečnosti se nelze spolehnout na teoretické kalibrační parametry a je potřeba provést kalibraci pomocí dvou či tří roztoků o známých hodnotách pH. Moderní přístroje podle změřených hodnot vypočítají směrnici kalibrační přímky (slope), obecně pro nelineární závislosti citlivost elektrody, současně se provádí i korekce na teplotu. Tyto „kalibrační parametry“ si přístroj „zapamatuje“ a změřená data podle nich zpracuje. Kalibrace se musí pravidelně opakovat, a to tím častěji, čím je elektroda starší. Zároveň je třeba dbát na to, aby kalibrace probíhala za stejných podmínek jako reálné měření (vodné prostředí, nevodné prostředí, obsah alkoholu apod.). Dalších nepřesností, které je třeba brát v potaz, se dopouští skleněná elektroda v kyselé a alkalické oblasti pH (Alkalická (pozitivní) chyba – v silně alkalické oblasti a kyselá (negativní) chyba při pH < 1).

Důležitým parametrem je též časová konstanta odpovědi, u skleněné elektrody zpravidla kolem 15 až 60 s. Délka odpovědi může být negativně ovlivněna i složením roztoku – např. koloidy a koncentrací měřeného iontu – rovnováha se ustaluje mnohonásobně déle.

Elektrolýza

[ ✎ upravit vložený článek ]

Ve výkladu elektrodových dějů jsme předpokládali, že soustava je v rovnovážném stavu. Zabývejme se nyní tím, co se stane, pokud na elektrody přivedeme napětí z vnějšího zdroje (elektrolytický článek, ΔG > 0). Probíhající děje se budou řídit Faradayovými zákony. K tomu, aby elektrolytické reakce začaly probíhat, musí napětí na elektrodách přesáhnout určitou hodnotu – rozkladné napětí (odpovídá součtu standardních elektrodových potenciálů pro jednotlivé reakce).

Jako příklad použijeme soustavu složenou z dvou inertních (platinových) elektrod ve vodném roztoku chloridu sodného.

Obecné schéma elektrolýzy.

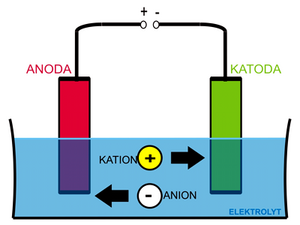
Vložíme-li na elektrody napětí, začnou ionty v roztoku putovat podle svého náboje, kationty Na⁺ a H⁺ ke katodě a anionty Cl⁻ a OH⁻ k anodě. Na katodě (a v její těsné blízkosti) budou probíhat reakce:

2 H⁺ + 2 e⁻ → H₂ ↑

a (při vyšším napětí):

Na⁺ + e⁻ → Na

2 Na + 2 H₂O → 2 Na⁺ + 2 OH⁻ + H₂ ↑

Na anodě bude probíhat reakce:

2 OH⁻ → H₂O + ½ O₂ ↑ + 2 e⁻

a (při vyšším napětí):

2 Cl⁻ → Cl₂ + 2 e⁻

Chlór se částečně uvolní jako plyn, částečně bude dále reagovat s vodou za vzniku kyseliny chlorovodíkové a kyseliny chlorné:

Cl₂ + H₂O → H⁺ + Cl⁻ + HClO

Vznikající plyny budou ze systému unikat (v tomto případě jde tedy o nevratný děj). Uvedený příklad známe i z praxe – všimněte si např. bublinek u elektrod při elektroforéze.

Využití

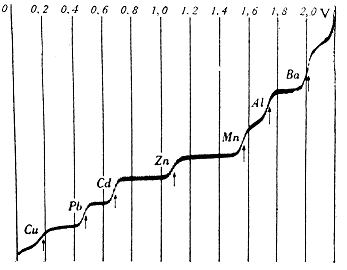
Polarografická křivka, závislost proudu na napětí. Převzato z

Tohoto jevu se využívá např. i v polarografii. Zjednodušeně řečeno, pokud budeme postupně zvyšovat napětí na elektrodách, bude soustavou zpočátku protékat jen malý proud. Po dosažení rozkladného napětí, charakteristického pro příslušný redoxní pár, začnou probíhat elektrolytické děje na povrchu měrné elektrody a proud se prudce zvýší (vzestupná část polarografické křivky). Jelikož tato reakce je velmi rychlá, dojde záhy k vyčerpání iontů v okolí elektrody. Nové ionty se k povrchu elektrody dostávají difuzí, jejíž rychlost je omezená, takže se intenzita proudu příliš nemění (rovné plato). Sestrojíme-li graf závislosti proudu na vloženém napětí, dostaneme schodovitou polarografickou křivku.

Odkazy

Související články

• Elektrodový potenciál
• pH
• pH silných kyselin a zásad
• pH slabých kyselin a zásad
• Měření pH

Použitá literatura

• NAVRÁTIL, T. a I.M MALBOHAN. Fyzikální a analytická chemie [online]. [cit. 2009-08-02]. <http://biochemie.euweb.cz/Biochemie/Fyzikal_chemie.zip>.

• LIMOJOE,. Pufr [online]. [cit. 2009-08-31]. <https://cs.wikipedia.org/wiki/Pufr>.

• KRAML, J, et al. Odměrná analýza II : Návody k praktickým cvičením z lékařské biochemie. 1. vydání. Praha. 1999. s. 59-63. ISBN 80-246-0020-X.

• KLOUDA, P. Moderní analytické metody. 1. vydání. Ostrava. 1996. ISBN 80-902155-0-5.

• VEJRAŽKA, Martin. Elektrochemie [online]. [cit. 2009-08-02]. <https://portal.lf1.cuni.cz/clanek-819-elektrochemie>.

• ŠPIČKA, Ladislav. Elektrolýza [online]. [cit. 2009-08-02]. <http://wwwold.tf.czu.cz/scripta/chemie4.rtf>.

• KOTOUČEK, M, J SKOPALOVÁ a P ADAMOVSKÝ. Příklady z analytické chemie [online]. Univerzita Palackého, [cit. 2009-08-31]. <http://ach.upol.cz/ucebnice/>.

• KOTOUČEK, M, J SKOPALOVÁ a P ADAMOVSKÝ. Výpočty z elektroanalytických metod [online]. Univerzita Palackého, [cit. 2009-08-31]. <http://ach.upol.cz/ucebnice2/>.