Reakční rychlost

Studiem reakční rychlosti se zabývá chemická kinetika.

Aby mohly spolu dvě či více látek reagovat, musí dojít ke srážce jejich molekul. Pravděpodobnost srážky se zvyšuje s rostoucí teplotou, tlakem a koncentrací látek.

Reakční rychlost (v) můžeme definovat jako rychlost úbytku reaktantů či rychlost přírůstku produktů, tedy např. pro reakci a A + b B → c C + d D:

$v=-{\frac {1}{a}}\cdot {\frac {d[A]}{dt}}=-{\frac {1}{b}}\cdot {\frac {d[B]}{dt}}={\frac {1}{c}}\cdot {\frac {d[C]}{dt}}={\frac {1}{d}}\cdot {\frac {d[D]}{dt}}$

Zabývejme se podrobněji vztahem mezi rychlostí reakce a koncentrací reaktantů. Uvažujme jednoduchou reakci X → Y. Její rychlost bude úměrná [X] podle rovnice:

(15)

$v=-{\frac {d[X]}{dt}}=k\cdot [X]$

kde k je rychlostní konstanta.

V některých případech může být rychlost úměrná [X]², může na [X] záviset složitěji, nebo naopak nemusí být na [X] závislá vůbec vůbec (v takovém případě probíhá reakce konstantní rychlostí). Přesný vztah mezi reakční rychlostí a koncentrací reaktantů je empirický fakt a – zejména bereme-li v úvahu reakce se složitějšími reakčními mechanismy – nedá se odvodit jen ze stechiometrie pozorované přeměny.

Chemici definují kinetický řád reakce podle počtu členů, jejichž koncentrace ovlivňují rychlost. Pokud rychlost na koncentraci nezávisí, a tedy platí rovnice v = k, hovoříme o řádu nultém. Je-li rychlost přímo úměrná koncentraci jednoho z reaktantů, jedná se o kinetiku prvního řádu (jako v případě výše uvedené reakce (15)). Jestliže je rychlost ovlivněna koncentrací dvou reaktantů nebo se jedná o exponenciální vztah jednoho reaktantu (v = k · [X] · [Y] nebo v = k · [X]²), hovoříme o kinetice druhého řádu atd.

Někdy chceme předpovědět, jaké množství reaktantu X zůstane nezreagováno po čase t od začátku reakce, nebo jak dlouho potrvá, než [X] klesne na polovinu. Při reakcích nultého řádu je výpočet jednoduchý, ale pro řády vyšší se komplikuje.

Pro reakci prvního řádu platí:

(16)

$-{\frac {d[X]}{dt}}=k\cdot [X]$

Integrací rovnice (16) dostáváme:

$-{\frac {1}{[X]}}\cdot {\frac {d[X]}{dt}}=k\cdot [X]$

$-\int {{\frac {1}{[X]}}\cdot {\frac {d[X]}{dt}}}=\int {k\cdot [X]}$

(17)

$-ln[X]=k\cdot t+c$

Řešením pro počátek reakce, tj. pro t = 0 (přičemž výchozí koncentraci látky X v tomto čase označíme jako [X]₀) dostáváme

(18)

$c=-ln[X]_{0}$

$-ln[X]=k\cdot t-ln[X]_{0}$

$-ln[X]+ln[X]_{0}=k\cdot t$

$-ln{\frac {[X]}{[X]_{0}}}=k\cdot t$

${\frac {[X]}{[X]_{0}}}=e^{-k\cdot t}$

(19)

$[X]=[X]_{0}\cdot e^{-k\cdot t}$

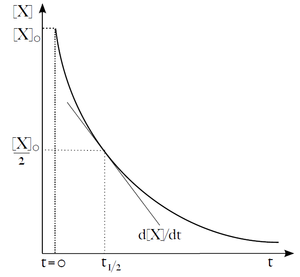
Tato rovnice popisuje exponenciální pokles koncentrace X v čase. Užitečným parametrem exponenciálního rozkladu je čas potřebný na snížení počáteční koncentrace (či množství) látky X na polovinu. Nazývá se poločas (t_1/2). Z rovnice (19) můžeme poločas vyjádřit jako:

$t_{1/2}={\frac {ln2}{k}}$